观测值聚类示例

一家体育用品公司的设计师想检验一款新型足球守门员手套。他让 20 名运动员穿戴新型手套，并收集运动员的性别、身高、体重和用手习惯信息。设计师想根据运动员的相似点来对其进行分组。

解释结果

该表格显示每步合并的聚类、聚类之间的距离和聚类的相似性。

到步骤 15 为止，相似性水平以大约 3 或更少的增量下降。当聚类数从 4 变为 3 时，相似性在步骤 16 和 17 的减少量超过 20（从 62.0036 到 41.0474）。
合并聚类之间的距离先减少约 0.6 或更少。当聚类数从 4 变为 3 时，距离在步骤 16 和 17 的增量超过 1（从 1.81904 到 2.82229）。

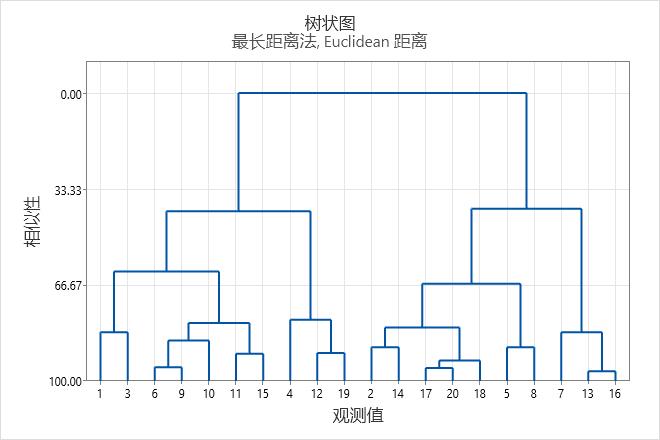
距离和相似性结果表明 4 个聚类对于最终分割是足够的。如果设计人员认为此分组具有直观意义，则这可能是个不错的选择。树状图以树形图的形式显示表格中的信息。

设计人员应重新运行分析，并在最终分割中指定 4 个聚类。当您指定最终分割时，Minitab 会显示附加的表格，描述最终分割中包含的每个聚类的特征。

步骤	点群数	相似性水平	距离水平	已合并的点群号		新聚类号	新聚类号中的观测值个数
1	19	96.6005	0.16275	13	16	13	2
2	18	95.4642	0.21715	17	20	17	2
3	17	95.2648	0.22669	6	9	6	2
4	16	92.9178	0.33905	17	18	17	3
5	15	90.5296	0.45339	11	15	11	2
6	14	90.3124	0.46378	12	19	12	2
7	13	88.2431	0.56285	2	14	2	2
8	12	88.2431	0.56285	5	8	5	2
9	11	85.9744	0.67146	6	10	6	3
10	10	83.0639	0.81080	7	13	7	3
11	9	83.0639	0.81080	1	3	1	2
12	8	81.4039	0.89027	2	17	2	5
13	7	79.8185	0.96617	6	11	6	5
14	6	78.7534	1.01716	4	12	4	3
15	5	66.2112	1.61760	2	5	2	7
16	4	62.0036	1.81904	1	6	1	7
17	3	41.0474	2.82229	1	4	1	10
18	2	40.1718	2.86421	2	7	2	10
19	1	0.0000	4.78739	1	2	1	20