什么是因子设计?
因子设计是一种设计试验,用于同时研究多个因子对响应的可能效应。在执行试验时,同时改变所有因子的水平(而不是一次改变一个)允许您研究因子之间的交互作用。
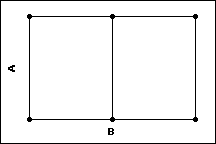
双因子设计
- 因子 A 的 2 个水平
- 因子 B 的 3 个水平
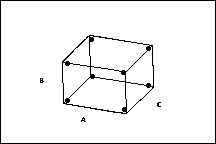
3 因子设计
每个因子的 2 个水平
可以运行全因子设计,也可以运行因子设计的一部分。
注意
当您拥有具有中心点的因子设计时,可以检验响应曲面的弯曲。但是,您无法对中心点以外任何其他位置的弯曲进行建模。换句话说,您只能计算设计中角点和中心点处的拟合值,因此无法创建等值线图。模型中必须有二次项(例如,平方项),才能对整个响应曲面的弯曲进行建模。对于响应曲面设计可以这样做。您可以使用轴点增强因子设计,以便从因子设计创建中心复合响应曲面设计。
什么是完全因子设计和部分因子设计?
全因子设计
全因子设计是研究人员将以因子水平的全部组合度量响应的设计。Minitab 提供两种类型的全因子设计:
- 二水平全因子设计:仅包含二水平因子。
- 一般全因子设计:包含具有两个以上水平的因子。
两水平全因子设计所需的试验次数为 2k,其中 k 为因子数。随着二水平因子设计中的因子数增加,执行全因子设计所必需的试验次数也将快速增加。例如,有 6 个因子的二水平全因子设计需要 64 次试验;有 9 个因子的设计需要 512 次试验。1/2 部分的部分因子设计只需要这些试验的一半。
部分因子设计
部分设计是实验者只执行全因子设计中的选定试验游程子集或部分试验游程的设计。当资源有限或设计中的因子数很大时,部分因子设计是一种很好的选择,因为它们比全因子设计使用的试验次数要少。
部分因子设计使用全因子设计的子集,因此一些主效应与双向交互作用混杂,而且不能与高阶交互作用的效应中分开。通常,试验中会假设高阶效应可忽略,以便通过少数几个游程获得有关主效应和低阶交互作用的信息。
什么是二水平全因子设计?
在二水平全因子设计中,每个试验因子都只有两个水平。整个试验包括这些因子水平的所有组合。虽然二水平因子设计无法完全考察因子空间中的广阔区域,但它们可以按因子提供相对较少试验次数的有用信息。由于二水平因子设计可以标识主要趋势,因此您可以使用它们来为其他试验提供方向。例如,需要进一步考察认为其中可能存在最优设置的区域时,可以增加一个因子设计形成中心复合设计。
比较
下图显示了全因子设计与 ½ 部分因子设计的比较。
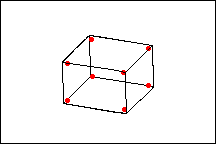
全因子设计
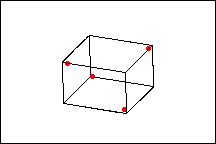
½ 部分因子设计
全因子设计包含的设计点是 ½ 部分设计中所包含设计点的两倍。后者仅在设计因子部分可能有的 8 个角点中的 4 个测量了响应。但是,使用此设计时,主效应将与双因子交互作用混杂。
Minitab 如何排序设计中的各个部分
| 部分 | 标准 (Yates) 顺序 | 设计生成元 |
|---|---|---|
| 1 | – – – | D = –AB, E = –AC, F = –BC |
| 2 | + – – | D = +AB, E = –AC, F = –BC |
| 3 | – + – | D = –AB, E = +AC, F = –BC |
| 4 | + + – | D = +AB, E = +AC, F = –BC |
| 5 | – – + | D = –AB, E = –AC, F = +BC |
| 6 | + – + | D = +AB, E = –AC, F = +BC |
| 7 | – + + | D = –AB, E = +AC, F = +BC |
| 8 | + + + | D = +AB, E = +AC, F = +BC |
主要部分始终是最后一个部分,并且具有所有 + 符号。
| 游程 | A | B | C | D = AB | E = –AC | F = –BC |
|---|---|---|---|---|---|---|
| 1 | – | – | – | + | – | – |
| 2 | + | – | – | – | + | – |
| 3 | – | + | – | – | – | + |
| 4 | + | + | – | + | + | + |
| 5 | – | – | + | + | + | + |
| 6 | + | – | + | – | – | + |
| 7 | – | + | + | – | + | – |
| 8 | + | + | + | + | – | – |
选择非默认的部分
创建部分因子设计时,默认情况下 Minitab 使用主要部分。主要部分是所有符号都为正的部分。但是,在某些情况下,设计所包含的点对每次试验而言可能不现实,而选择适当的部分可以避免这些点。
- D = –AB E = –AC
- D = AB E = –AC
- D = –AB E = AC
- D = AB E = AC
例如,假设无法以在其高水平设置的所有五个因子执行前一示例中的设计。主要部分包含此点,但第三个部分则不然。
