筛选设计
筛选设计是一种类型的设计试验,通常用于确定过程中最重要的因子。有了筛选设计,可以使用相对较少的、具有许多潜在因子的游程来确定数量较少的、会影响过程质量的最重要因子。在执行筛选试验之后,可以在许多更多详细信息时执行优化试验。例如,假设您要检查会影响冰淇淋质地的各种因子:脂肪含量、巴氏灭菌法温度、均匀化过程、混合速度、提取温度、乳化剂、稳定剂和冷却速度。您可以使用筛选设计来识别会影响冰淇淋质地的最重要因子。必要时,可以使用较大的因子设计或响应曲面设计来优化过程。
- 明确筛选设计
- 明确筛选设计是一种筛选设计,其中的每个连续因子中包含 3 个水平,以便它们可以估计平方项和线性项。由于线性项与任何二因子交互作用不互为别名,因此,明确筛选设计还允许您查找可能重要的交互作用的证据。例如,使用 8 个因子,明确筛选设计可以为 3 个或更少的重要因子高效地拟合所有线性、平方和双因子交互作用。
- Plackett-Burman 设计
-
Plackett-Burman 设计通常是解析度 III 二水平设计。在解析度 III 设计中,主效应与双因子交互作用互为别名。因此,应该只在假设双因子交互作用可以忽略时才使用这些设计。由于此假设,Plackett-Burman 设计的游程数可以比明确筛选设计的游程数少。如果您在完成 Plackett-Burman 设计之后怀疑有交互作用,则可以折叠设计,这会使游程数加倍。在折叠 Plackett-Burman 设计之后,主效应不与双因子交互作用互为别名。有关更多信息,请转到什么是折叠?。
因子设计
- 二水平因子设计(默认生成元)
- 选择此选项可以创建全因子设计或创建部分因子设计。默认生成元将创建对于因子数和游程数具有最高分辨度的设计。
- 二水平因子设计(指定生成元)
- 在部分因子设计中,可以使用自定的生成元指定运行哪些特定的子集。还可以通过指定生成元来添加因子以及通过指定项的生成元来定义区组。
- 二水平裂区设计(难以改变的因子)
- 至少包括一个很难改变水平的因子,因而由于时间或成本约束而难以完全随机化的试验设计。
- Plackett-Burman 设计
-
Plackett-Burman 设计通常是解析度 III 二水平设计。在解析度 III 设计中,主效应与双因子交互作用互为别名。因此,应该只在假设双因子交互作用可以忽略时才使用这些设计。
使用 Plackett-Burman 设计可以在试验阶段的早期识别出最重要的因子。例如,假设您要检查会影响冰淇淋质地的各种因子:脂肪含量、巴氏灭菌法温度、均匀化过程、混合速度、提取温度、乳化剂、稳定剂和冷却速度。可以使用 Plackett-Burman 试验来确定最重要的主效应,使用因子或全因子设计进一步研究它们,然后使用响应曲面设计来优化您的过程。
- 一般全因子设计
- 因子可以具有任意数量水平的试验设计。因子全部是类别因子。
响应曲面设计
- 中心复合
- 通过将中心点和轴点添加到 2 水平因子中来对弯曲建模的试验设计。
- Box-Behnken
- Box-Behnken 设计的设计点通常比中心复合设计少,因此在因子数相同的情况下,它们的运行成本较低。它们可以高效估计一阶和二阶系数,但是它们不能包括来自因子试验的游程。与中心复合设计不同的是,Box-Behnken 设计中的每个因子始终有 3 个水平,而中心复合设计中最多可以有 5 个水平。与中心复合设计的另一个区别是,Box-Behnken 设计从不包括其所有因子均处于极值设置(例如,所有的因子都处于低设置)的游程。
混料设计
混料试验是一类特殊的响应曲面试验,其中所调查的产品由多种成分组成。设计这些试验很有用,因为工业环境下许多产品设计和开发活动都涉及配方或混料。在这些环境中,响应是混料中各种成分的比例的函数。例如,您可能正在开发一种由面粉、发酵粉、牛奶、鸡蛋和食用油组成的薄饼配方。或者可能正在开发混合四种化学成分的杀虫剂。有关混料设计的更多信息,请转到 什么是混料设计?
在最简单的混料试验中,响应(基于某些标准的产品质量或性能)取决于这些分量(成分)的相对比例。分量的量(以重量、体积或某些其他单位来度量)相加后得出标准总量。相比较而言,因子设计中的响应则随每个因子的数量而变化。
| 未增强 | 已增强 | |
| 单纯形质心 |
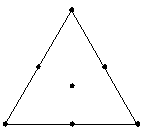 可以拟合最高为特殊立方的模型。 |
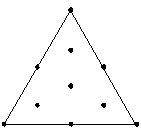 可以部分拟合最高为完整立方的模型。 |
| 单纯形格点格度 1 |
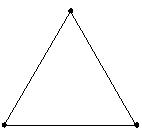 可以拟合线性模型。 |
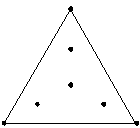 可以部分拟合最高为二次的模型。 |
| 单纯形格点格度 2 |
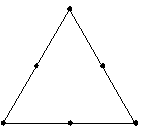 可以拟合最高为二次的模型。 |
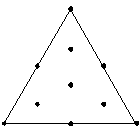 可以部分拟合最高为特殊立方的模型。 |
| 单纯形格点格度 3 |
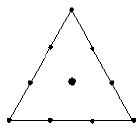 可以拟合最高为完整立方的模型。 |
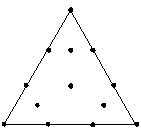 可以拟合最高为完整立方的模型。 |
- 单纯形质心
- 设计点以均匀方式(或格点)在 L 单纯形中排列的混料设计。使用单纯形质心设计可以估计最高阶与多个分量的阶相同的项。对于小型设计,可以使用单纯形格点设计,这将使估计的项限制为更低阶的项。

可以使用此单纯形质心设计最高为特殊立方的模型。
- 单纯形格点
- 设计点以均匀方式(或格点)在 L 单纯形中排列的混料设计。格点的阶数(格度)决定拟合的项的阶数。

格度为 1 的格点设计其运行次数比单纯形质心设计少,但是仍可以估计简单模型。

格度为 1 的格点设计其运行次数比单纯形质心设计多,因此可以估计较复杂的模型。
- 极端顶点
-
仅在单纯形中包含子部分或较小空间的混料设计。
极端顶点设计的目标是选择可以充分覆盖设计空间的设计点。下图显示了同时具有上限和下限约束的两个三分量设计的极端顶点:
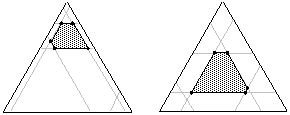
浅灰色线表示分量的下限和上限约束。深灰色区域表示设计空间。点放置在设计空间的极端顶点处。
田口设计
田口设计是可以选择在操作环境中更加稳定运行的产品或过程的试验设计。田口设计认识到,并非所有引起变异的因子都可以得到控制。这些无法控制的因子称为噪声因子。田口设计尝试确认使噪声因子的效应最小化的可控制因子(控制因子)。在试验中,对噪声因子进行操作以强制产生变异,然后确定使过程或产品稳健(即对来自噪声因子的变异有抵抗力)的最优控制因子设置。以此目标设计的过程会产生更一致的输出。以此目标设计的产品可以提供更一致的性能,而无论使用该产品的环境如何。
田口设计的著名示例来自 20 世纪 50 年代日本的 Ina Tile 公司。该公司制造了大量非指定尺寸的瓷砖。质量小组发现,用于烧制瓷砖的窑中的温度发生了变化,从而导致了瓷砖的尺寸不均匀。由于建造新窑的成本很高,因此无法消除温度变异。这样,温度就成了噪声因子。使用田口设计的试验,小组发现通过增加粘土的石灰含量(一个控制因子),瓷砖对窑内温度变异更具抵抗力(即更稳健),使其可以生产出更均匀的瓷砖。
- 二水平设计
- 每个控制因子只有 2 个水平的试验设计。
- 3 水平设计
- 每个控制因子刚好有 3 个水平的试验设计。
- 4 水平设计
- 每个控制因子刚好有 4 个水平的试验设计。
- 5 水平设计
- 每个控制因子刚好有 5 个水平的试验设计。
- 混合水平设计
- 控制因子有不同数量的水平的试验设计。
