设计矩阵
首先,Minitab 会根据您指定的因子以及模型创建一个设计矩阵。此矩阵的列表示模型中的项。然后,Minitab 为常量项、区组和高阶项添加列以完成分析中模型的设计矩阵。
具有所有连续因子的设计
设计矩阵的形式取决于是否存在行数等于因子数的会议矩阵。当此条件为真时,设计矩阵中表示因子的列采用如下形式:
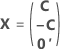
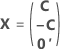
其中 C 是 n × n 会议矩阵,其中包含满足如下属性的单元 {-1, 0, 1}:
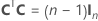
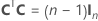
当不存在具有正确大小的会议矩阵时,表示因子的列是大会议矩阵的子集:
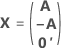
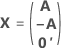
其中 A 是 N × n 矩阵,其中包含满足以下属性的单元 {-1, 0, 1}:
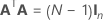
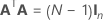
完整设计矩阵除了包含表示因子的列,还包含其他列。设计矩阵包含一个全是 1(表示常量项)的列。完整设计矩阵还包括表示模型中任何平方项或交互作用项的列。
具有类别因子的设计
对于包括类别因子的设计,Minitab 将设计矩阵中的单中心点行替换为 2 个伪中心点。如果设计中只有 1 个类别因子,则仅存在两个可能的伪中心点,因此这两个点均在设计中。
如果设计中有 2 个以上的类别因子,则 Minitab 将使用迭代算法选择要包括的 2 个伪中心点。该算法设法最小化模型中线性效应的回归系数方差。
表示法
| 项 | 说明 |
|---|---|
| C | 会议矩阵 |
| 0' | 矩阵中由表示中心点游程的零组成的行 |
| In | n × n 单位矩阵 |
| A | 包含 N 行和 n 列的会议矩阵的子集,其中, |
| N | 会议矩阵中列子集中的行数 |
| n | 设计中的因子数 |
系数 (Coef)
在矩阵项中,计算模型中系数向量的公式为:

表示法
| 项 | 说明 |
|---|---|
| X | 设计矩阵 |
| Y | 响应向量 |
Box-Cox 变换
Box-Cox 变换选择能够最小化残差平方和的 lambda 值(如下所示)。由此生成的变换是 Yλ(当 λ ≠ 0 时)及 ln(Y)(当 λ = 0 时)。当 λ < 0 时,Minitab 还会将变换后响应乘以 −1,以维持未变换响应的顺序。
Minitab 搜索介于 −2 和 2 之间的最优值。此区间以外的值生成的拟合可能较差。
以下是一些常见的变换,其中 Y' 是数据 Y 的变换:
| Lambda (λ) 值 | 变换 |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = .5 | Y′ = 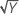 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −.5 |  |
| λ = −1 | Y′ = −1 / Y |
加权回归
加权最小二乘回归是处理具有非恒定方差的观测值的方法。如果方差不是恒定的,则观测值应具备以下特点:
- 应当为较大的方差指定相对较小的权重
- 应当为较小的方差指定相对较大的权重
权重的常用选项是响应中纯误差方程之逆。
估计系数的公式如下所示:
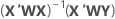
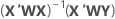
这相当于将加权 SS 误差最小化。
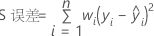
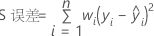
表示法
| 项 | 说明 |
|---|---|
| X | 设计矩阵 |
| X' | 转置设计矩阵 |
| W | 对角线上的 n x n 权重矩阵 |
| Y | 响应值向量 |
| n | 观测值个数 |
| wi | 第 i 个响应值的权重 |
| yi | 第 i 个观测值的响应值 |
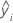 | 第 i 个观测值的拟合值 |
