拟合
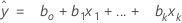
表示法
| 项 | 说明 |
|---|---|
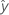 | 拟合值 |
| xk | 第 k 个项。每个项都可以是单个预测变量、多项式项或交互作用项。 |
| bk | 第 k 个回归系数的估计值 |
拟合值的标准误(拟合值 SE)
具有一个预测变量的回归模型中拟合值的标准误为:

具有多个预测变量的回归模型中拟合值的标准误为:

对于加权回归,在公式中包括权重矩阵:

当数据具有测试数据集或 K 折交叉验证时,公式相同。的值 s2 是从培训数据。设计矩阵和重量矩阵也来自训练数据。
表示法
| 项 | 说明 |
|---|---|
| s2 | mean square error |
| n | number of observations |
| x0 | new value of the predictor |
 | mean of the predictor |
| xi | i(序号) predictor value |
| x0 | vector of values that produce the fitted values, one for each column in the design matrix, beginning with a 1 for the constant term |
| x0 | transpose of the new vector of predictor values |
| X | design matrix |
| W | weight matrix |
残差
残差是观测值与相应拟合值之间的差分。该模型不解释这部分观测值。观测值的残差为:
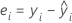
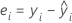
表示法
| 项 | 说明 |
|---|---|
| yi | 观测的第 i 个响应值 |
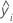 | 第 i 个响应拟合值 |
标准化残差
标准化残差也称为“内部 t 化残差”。
公式

表示法
| 项 | 说明 |
|---|---|
| ei | 第 i 个残差 |
| hi | X(X'X)–1X' 的第 i 个对角线元素 |
| s2 | 均方误 |
| X | 设计矩阵 |
| X' | 转置设计矩阵 |
删后(t 化)残差
也称为外部 t 化残差。公式为:
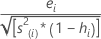
此公式的其他表现形式为:

估计第 i 个观测值的模型会从数据集中忽略第 i 个观测值。因此,第 i 个观测值无法对估计值产生影响。每个删后残差均具有学生 t 分布,其中具有 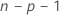 自由度。
自由度。
表示法
| 项 | 说明 |
|---|---|
| ei | 第 i 个残差 |
| s(i)2 | 未使用第 i 个观测值计算得出的均方误差 |
| hi | X(X'X)–1X' 的第 i 个对角线元素 |
| n | 观测值个数 |
| p | 项数,包括常量 |
| SSE | 误差平方和 |
置信区间
一组给定预测变量值的估计平均响应将落入的范围。
公式
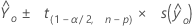
表示法
| 项 | 说明 |
|---|---|
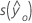 |  |
 | 一组给定预测变量值的拟合响应值 |
| α | 类型 I 误差率 |
| n | 观测值个数 |
| p | 模型参数个数 |
| S 2(b) | 系数的方差-协方差矩阵 |
| s 2 | 均方误 |
| X | 设计矩阵 |
| X0 | 给定预测变量值的矢量,具有 1 列和 p 行 |
| X'0 | 具有 1 行和 p 列的预测变量值的新矢 量的转 置 |
预测区间
预测区间是新观测值的拟合响应预计将落入的范围。
公式
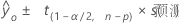
Notation
| 项 | 说明 |
|---|---|
| s(Pred) |  |
 | 一组给定预测变量值的拟合响应值 |
| α | 显著性水平 |
| n | 观测值个数 |
| p | 模型参数个数 |
| s 2 | 均方误 |
| X | 预测变量矩阵 |
| X0 | 给定预测变量值的矢量,具有 1 列和 p 行 |
| X'0 | 具有 1 行和 p 列的预测变量值的新矢 量的转 置 |
