步骤 1:确定哪些项对响应变异性的贡献最大
使用 Pareto 标准化效应图可比较效应的相对量值与统计显著性。
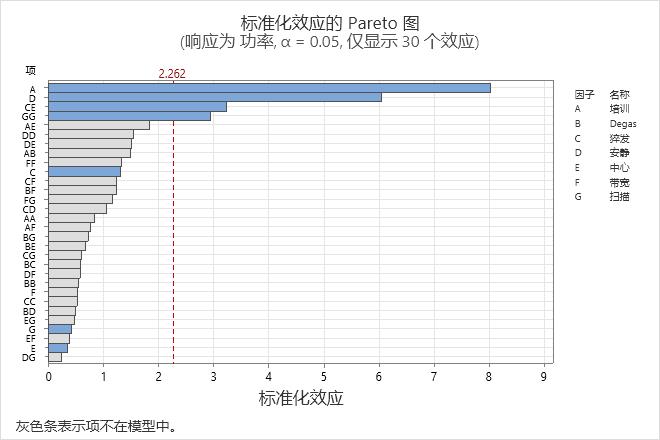
Minitab 按照标准化效应绝对值的递减顺序绘制标准化效应图。图中的参考线表明哪些效应在统计意义上显著。
主要结果:Pareto 图
在这些结果中,模型中的项具有蓝色条。不在模型中的项具有灰色条。该图显示在 α = 0.05 的显著性水平下 2 个主效应在统计意义上显著。一个二次项和一个交互作用效应也很显著。属于交互作用和二次项的主效应位于模型中,即使这些效应在统计意义上不显著时也是如此。
此外,还可以发现最大的效应是 A,因为它延伸得最远。EE 二次项的效应是图上的最小效应。
步骤 2:确定哪些项对响应具有统计意义显著的效应
- P 值 ≤ α:关联在统计意义上显著
- 如果 P 值小于或等于显著性水平,则可以得出响应变量与项之间的关联在统计意义上显著的结论。
- P 值 > α:关联在统计意义上不显著
- 如果 p 值大于显著性水平,则无法得出响应变量与该项之间的关联在统计意义上显著的结论。您可能希望重新拟合没有该项的模型。
- 因子数
- 如果因子的系数在统计意义上显著,则可以得出因子的系数不等于 0 的结论。
- 因子之间的交互作用
- 如果一个交互作用的系数在统计意义上显著,则可以得出结论:因子与响应之间的关系取决于该项中的其他因子。
- 二次项
- 如果一个二次项的系数在统计意义上显著,则可以得出结论:响应曲面中包含弯曲。
- 协变量
- 如果一个协变量的系数在统计意义上显著,则可以得出结论:响应与协变量之间的关联在统计意义上显著。
- 区组
- 如果一个区组的系数在统计意义上显著,则可以得出结论:该区组中响应均值与总体响应均值不同。
已编码系数
| 项 | 系数 | 系数标准误 | T 值 | P 值 | 方差膨胀因子 |
|---|---|---|---|---|---|
| 常量 | 617.1 | 15.0 | 41.16 | 0.000 | |
| 培训 | 52.41 | 6.53 | 8.02 | 0.000 | 1.00 |
| 猝发 | 8.62 | 6.53 | 1.32 | 0.220 | 1.00 |
| 安静 | -39.59 | 6.53 | -6.06 | 0.000 | 1.00 |
| 中心 | -2.36 | 6.53 | -0.36 | 0.727 | 1.00 |
| 扫描 | 2.84 | 6.53 | 0.44 | 0.674 | 1.00 |
| 扫描*扫描 | 49.4 | 16.7 | 2.95 | 0.016 | 1.16 |
| 猝发*中心 | 24.63 | 7.59 | 3.25 | 0.010 | 1.16 |
主要结果:P 值、系数
在这些结果中,在 0.05 水平下,“培训”和“安静”的主效应在统计意义上显著。您可推断出这些变量的变化是与响应变量的变化相关的。
“扫描”的主效应在统计意义上不显著,但二次效应在统计意义上显著。您可推断出此变量的变化与响应变量的变化相关联,但这种关联不是线性的。
“猝发”和“中心”的主效应在统计意义上不显著,但交互作用效应在统计意义上显著。您可推断出这些变量的变化与响应变量的变化相关联,但这些效应取决于其他因子。
步骤 3:确定模型对数据的拟合优度
要确定模型与数据的拟合优度,请检查模型汇总表中的拟合优度统计量。
- S
-
使用 S 可评估模型描述响应值的程度。
S 以响应变量的单位进行度量,它表示数据值与拟合值的距离。S 值越低,模型描述响应的程度越高。但是,自身低 S 值并不表明模型符合模型假设。您应检查残差图来验证假设。
- R-sq
-
R2 值越高,模型拟合数据的优度越高。R2 始终介于 0% 和 100% 之间。
如果向模型添加其他预测变量,则 R2 会始终增加。例如,最佳的 5 预测变量模型的 R2 始终比最佳的 4 预测变量模型的高。因此,比较相同大小的模型时 R2 最有效。
- R-sq(调整)
-
在想要比较具有不同数量的预测变量的情况下,使用调整的 R2。如果向模型添加预测变量,即使模型没有实际改善,R2 也会始终增加。调整的 R2 值包含模型中的预测变量数,以便帮助您选择正确的模型。
- R-sq(预测)
-
使用预测的 R2 可确定模型对新观测值的响应进行预测的程度。具有较大预测 R2 值的模型的预测能力也较出色。
实质上小于 R2 的预测的 R2 可能表明模型过度拟合。在向总体中添加不太重要的影响项的情况下,可能会发生过度拟合模型。模型针对样本数据而定制,因此可能对于总体预测不太有效。
在比较模型方面,预测的 R2 还可能比调整的 R2 更有效,因为它是用模型计算中未包含的观测值计算得出的。
- AICc 和 BIC
- 当您显示逐步方法每个步骤的详细信息时或者显示分析的扩展结果时,Minitab 会多显示两个统计量。这些统计量是更正的 Akaike 信息标准 (AICc) 和 Bayesian 信息标准 (BIC)。使用这些统计量可以比较不同的模型。对于每个统计量,较小的值比较合意。
- 样本数量较小则不能提供对于响应变量和预测变量之间关系强度的精确估计。例如,如果需要 R2 更为精确,则应当使用较大的样本(通常为 40 或更多)。
- 拟合优度统计量只是模型拟合数据优度的一种度量。即使模型具有合意的值,您也应当检查残差图,以验证模型是否符合模型假设。
模型汇总
| S | R-sq | R-sq(调整) | R-sq(预测) |
|---|---|---|---|
| 24.4482 | 93.68% | 88.77% | 76.78% |
主要结果:S、R-sq、R-sq(调整)、R-sq(预测)
在这些结果中,模型解释了输出中 93.68% 的变异。对于这些数据,R2 值表明模型与数据优度拟合。如果要拟合具有不同项的其他模型,请使用调整的 R2 值和预测的 R2 值来比较模型与数据的拟合度
步骤 4:确定模型是否符合分析的假设条件
使用残差图可帮助您确定模型是否适用并符合分析的假设。如果不符合此假设,则模型可能无法充分拟合数据,在解释结果时应当格外小心。
有关如何处理残差图模式的更多信息,请转到分析明确筛选设计的残差图,然后单击页面顶部列表中残差图的名称。
残差与拟合值图
下表中的模式可能表示该模型不满足模型假设。| 模式 | 模式的含义 |
|---|---|
| 残差相对拟合值呈扇形或不均匀分散 | 异方差 |
| 曲线 | 缺少高阶项 |
| 远离 0 的点 | 异常值 |
| 在 X 方向远离其他点的点 | 有影响的点 |
使用残差与拟合值图可验证残差随机分布和具有常量方差的假设。理想情况下,点应当在 0 的两端随机分布,点中无可辨识的模式。
残差与顺序图
趋势
偏移
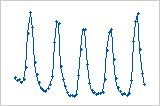
周期
残差的正态概率图
使用残差的正态概率图可验证残差呈正态分布的假设。残差的正态概率图应该大致为一条直线。
下表中的模式可能表示该模型不满足模型假设。
| 模式 | 模式的含义 |
|---|---|
| 非直线 | 非正态性 |
| 远离直线的点 | 异常值 |
| 斜率不断变化 | 未确定的变量 |
