步骤 1:确定哪些项对响应具有最大效应
使用 Pareto 标准化效应图可比较主效应、平方效应和交互作用效应的相对量值与统计显著性。
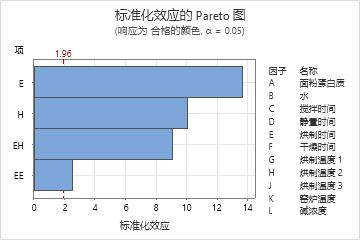
Minitab 按照标准化效应绝对值的递减顺序绘制标准化效应图。图中的参考线表明哪些效应是显著效应。默认情况下,Minitab 使用显著性水平 .05 绘制参考线。
主要结果:Pareto 图
在这些结果中,该图仅包括模型中的项。该图显示 2 个主效应在统计意义上显著。一个二次项和一个交互作用效应在统计意义上也很显著。
此外,还可以发现最大的效应是 E,因为它延伸得最远。最小的效应是 EE 二次项效应,因为它延伸得最近。
步骤 2:确定哪些项对响应具有统计意义显著的效应
- P 值 ≤ α:关联在统计意义上显著
- 如果 P 值小于或等于显著性水平,则可以得出响应变量与项之间的关联在统计意义上显著的结论。
- P 值 > α:关联在统计意义上不显著
- 如果 p 值大于显著性水平,则无法得出响应变量与该项之间的关联在统计意义上显著的结论。您可能希望重新拟合没有该项的模型。
- 因子
- 如果因子的系数显著,则可以断定并非所有因子水平都具有相同的事件概率。
- 因子之间的交互作用
- 如果一个交互作用项的系数显著,则因子与响应之间的关系取决于该项中的其他因子。在这种情况下,不应在不考虑交互作用效应时解释主效应。
- 二次项
- 如果一个平方项的系数在统计意义上显著,则可以得出结论:因子与响应之间的关系沿着曲线分布。
- 协变量
- 如果一个协变量的系数在统计意义上显著,则可以得出结论:响应与协变量之间的关联在统计意义上显著。
- 区组
- 如果区组的系数在统计意义上显著,则可以断定区组的链接函数与平均值不同。
已编码系数
| 项 | 系数 | 系数标准误 | 方差膨胀因子 |
|---|---|---|---|
| 常量 | 2.394 | 0.145 | |
| 烘制时间 | 0.7349 | 0.0538 | 1.11 |
| 烘制温度 2 | 0.5451 | 0.0541 | 1.20 |
| 烘制时间*烘制时间 | -0.384 | 0.153 | 1.04 |
| 烘制时间*烘制温度 2 | -0.5106 | 0.0562 | 1.24 |
主要结果:系数
在这些结果中,烘制时间和烘制温度 2的系数为正数。烘制时间的平方项系数为负数,烘制时间和烘制温度 2之间交互作用项的系数为负数。一般而言,在项的值增大时,正系数会使事件发生的可能性变大,负系数会使事件发生的可能性变小。
方差分析
| 来源 | 自由度 | 调整后偏差 | 调整后均值 | 卡方 | P 值 |
|---|---|---|---|---|---|
| 模型 | 4 | 737.452 | 184.363 | 737.45 | 0.000 |
| 烘制时间 | 1 | 203.236 | 203.236 | 203.24 | 0.000 |
| 烘制温度 2 | 1 | 100.432 | 100.432 | 100.43 | 0.000 |
| 烘制时间*烘制时间 | 1 | 6.770 | 6.770 | 6.77 | 0.009 |
| 烘制时间*烘制温度 2 | 1 | 80.605 | 80.605 | 80.61 | 0.000 |
| 误差 | 45 | 32.276 | 0.717 | ||
| 合计 | 49 | 769.728 |
主要结果:P 值
在这些结果中,在 0.05 水平下,烘制时间和烘制温度 2的主效应在统计意义上显著。您可推断出这些变量的变化是与响应变量的变化相关的。由于高阶项位于模型中,因此主效应的系数不能完全描述这些因子的效应。
烘制时间的平方项显著。您可推断出此变量的变化与响应变量的变化相关联,但这种关联不是线性的。
烘制时间和烘制温度 2之间的交互作用效应显著。您可以断定对烘制时间中更改颜色的效应取决于烘制温度 2的水平。同样,您可以断定对烘制温度 2中更改颜色的效应取决于烘制时间的水平。
步骤 3:了解预测变量的效应
- 连续预测变量的优势比
- 优势比大于 1 表示在预测变量越大,事件发生的几率越大。优势比小于 1 表示预测变量越大,事件发生的几率越小。
连续预测变量的优势比
变更单位 优势比 95% 置信区间 烘制时间 2 * (*, *) 烘制温度 2 15 2.1653 (1.9652, 2.3858) 主要结果:优势比
在这些结果中,模型有 3 个用来预测蝴蝶脆饼的颜色是否符合质量标准的项:烘制时间、烘制温度 2以及烘制时间的平方项。在此示例中,可接受的颜色为“事件”。
单位编号显示设计中一个编码单位的自然单位差异。例如,在自然单位中,烘制温度 2的低水平为 127。高水平为 157 度。从低水平到中点的距离表示 1 个编码单位的变化。在这种情况下,该距离为 15 度。
烘制温度 2的优势比大约为 2.17。温度每上升 15 度,蝴蝶脆饼颜色可接受的优势会增加大约 2.17 倍。
烘制时间的优势比缺少,这是因为模型中包含烘制时间的平方项。优势比的值不固定,这是因为优势比的值依赖烘制时间的值。
- 类别预测变量的优势比
-
对于类别预测变量,优势比可以比较事件在两个不同的预测变量水平发生的几率。Minitab 通过在水平 A 和水平 B 这两列中列出水平来设置比较。水平 B 是因子的参考水平。优势比大于 1 表示事件在水平 A 下发生的几率大。优势比小于 1 表示事件在水平 A 下发生的几率小。有关类别预测变量编码的更多信息,请转到类别预测变量的编码方案。
类别预测变量的优势比
水平 A 水平 B 优势比 95% 置信区间 月份 2 1 1.1250 (0.0600, 21.0834) 3 1 3.3750 (0.2897, 39.3165) 4 1 7.7143 (0.7461, 79.7592) 5 1 2.2500 (0.1107, 45.7172) 6 1 6.0000 (0.5322, 67.6397) 3 2 3.0000 (0.2547, 35.3325) 4 2 6.8571 (0.6556, 71.7169) 5 2 2.0000 (0.0976, 41.0019) 6 2 5.3333 (0.4679, 60.7946) 4 3 2.2857 (0.4103, 12.7323) 5 3 0.6667 (0.0514, 8.6389) 6 3 1.7778 (0.2842, 11.1200) 5 4 0.2917 (0.0252, 3.3719) 6 4 0.7778 (0.1464, 4.1326) 6 5 2.6667 (0.2124, 33.4861) 主要结果:优势比
在这些结果中,类别预测变量是距离酒店旺季开始时间的月份。响应是客户是否取消预定房间。在此示例中,取消预定房间为“事件”。当水平 A 为第 4 个月,水平 B 为第 1 个月时,最大的优势比大约为 7.71。这表示客户在第 4 个月取消预定房间的优势约为客户在第 1 个月取消预定房间的优势的 8 倍。
步骤 4:确定模型拟合数据的优度
要确定模型与数据的拟合优度,请检查模型汇总表中的拟合优度统计量。
注意
数据在工作表中的排列方式以及每行是存在一个还是多个试验会影响很多模型汇总和拟合优度统计量。Hosmer-Lemeshow 检验不会受数据排列方式影响,并且无论每行是存在一个还是多个试验都可进行比较。有关更多信息,请转到数据格式对二元 Logistic 回归中拟合优度的影响。
- 偏差 R-Sq
-
偏差 R2 值越高,模型拟合数据的优度越高。偏差 R2 始终在 0% 和 100%之间。
如果向模型添加其他项,则偏差 R2 会始终增加。例如,最佳的 5 项模型的偏差 R2 始终比最佳的 4 预测变量模型的高。因此,比较相同大小的模型时,偏差 R2 最有用。
数据排列会影响偏差 R2 值。每行有多个试验的数据通常比每行只有一个试验的数据具有更高的偏差 R2。偏差 R2 值仅在使用相同数据格式的模型之间可比较。
拟合优度统计量只是模型拟合数据优度的一种度量。即使模型具有合意的值,您也应当检查残差图和拟合优度检验,以评估模型拟合数据的优度。
- 偏差 R-sq (adj)
-
使用调整的偏差 R2 来比较具有不同项数的模型。如果向模型添加项,偏差 R2 也会始终增加。调整的偏差 R2 值在模型中包含了项数,以帮助您选择正确的模型。
- AIC、AICc 和 BIC
- 使用 AIC、AICc 和 BIC 比较不同的模型。对于每个统计量,较小的值比较合意。但是,对于预测变量集具有最小值的模型,不一定需要很准确地拟合数据。而且,还可使用拟合优度检验和残差图评估模型与数据的拟合优度。
模型汇总
| 偏差 R-Sq | 偏差 R-Sq (调整) | AIC | AICc | BIC |
|---|---|---|---|---|
| 95.81% | 95.16% | 243.85 | 245.80 | 255.32 |
主要结果:偏差 R-Sq、偏差 R-Sq (adj)、AIC、 AICc、BIC
在这些结果中,模型可以解释响应变量中 95.81% 的偏差。对于这些数据,偏差 R2 值表示模型与数据充分拟合。如果要拟合具有不同项的其他模型,请使用调整的偏差 R2 值、AIC 值、AICc 值和 BIC 值比较模型对数据的拟合优度。
步骤 5:确定模型是否无法与数据拟合
- 不正确的链接函数
- 忽略了模型中变量的高阶项
- 忽略了模型中不存在的预测变量
- 过度离散
如果偏离在统计上显著,则您可以尝试另一种链接函数或更改模型中的项。
- 偏差:与每行多个试验的数据相比,每行排列单个试验的数据的偏差检验 p 值往往较小。对于每行单个试验的数据,Hosmer-Lemeshow 结果更可靠。
- Pearson:如果数据中每行事件的预计数量较小,则 Pearson 检验使用的卡方分布近似不准确。因此,如果数据为每行一个试验的格式,则 Pearson 拟合优度检验也不准确。
- Hosmer-Lemeshow:Hosmer-Lemeshow 检验不像其他拟合优度检验那样依赖于数据中每行的试验数。当数据中每行的试验数很少时,Hosmer-Lemeshow 检验能够更可靠地指出模型对数据的拟合优度。
拟合优度检验
| 检验 | 自由度 | 卡方 | P 值 |
|---|---|---|---|
| 偏差 | 44 | 32.26 | 0.905 |
| Pearson | 44 | 31.98 | 0.911 |
| Hosmer-Lemeshow | 7 | 4.18 | 0.758 |
事件/试验格式的主要结果:响应信息、偏差检验、Pearson 检验、Hosmer-Lemeshow 检验
在这些结果中,所有拟合优度检验的 P 值都大于常见显著性水平 ..05。这些检验无法提供预测概率以二项分布无法预测的方式偏离观测概率的证据。
