质量工程师想要改进蝴蝶脆饼生产流程。颜色是关键的质量特征。工程师使用明确筛选设计以确定哪些潜在因子会影响蝴蝶脆饼的颜色。对于本试验,检查员按照符合标准或不符合标准对小批次的蝴蝶脆饼进行快速分类。
- 打开样本数据 蝴蝶脆饼颜色.MWX。
- 选择。
- 在事件名称中,输入事件。
- 在事件数中,输入合格的颜色。
- 在试验数中,输入试验次数。
- 单击项。
- 在包括以下项中,选择完全二次。单击确定。
- 单击逐步。
- 在方法中,选择转发信息标准。
- 单击每个对话框中的确定。
解释结果
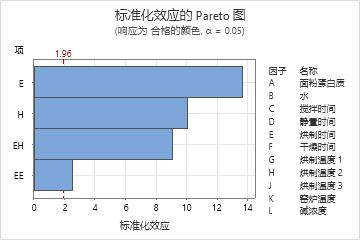
Pareto 图显示与最佳模型(按照 AICc 标准)中的项相对应的条。模型中的两个主效应:烘制时间 (E) 和 烘制温度 2 (H)。该模型还包括烘制时间的平方项,以及这两个因子之间的交互作用效应。
工程师同意此模型与其过程知识相匹配。工程师决定使用模型来规划进一步的试验。
响应信息
| 合格的颜色 | 事件 | 4235 | 事件 |
|---|
| | 非事件 | 765 | |
|---|
| 试验次数 | 合计 | 5000 | |
|---|
已编码系数
| 常量 | 2.394 | 0.145 | |
|---|
| 烘制时间 | 0.7349 | 0.0538 | 1.11 |
|---|
| 烘制温度 2 | 0.5451 | 0.0541 | 1.20 |
|---|
| 烘制时间*烘制时间 | -0.384 | 0.153 | 1.04 |
|---|
| 烘制时间*烘制温度 2 | -0.5106 | 0.0562 | 1.24 |
|---|
连续预测变量的优势比
| 烘制时间 | 2 | * | (*, *) |
|---|
| 烘制温度 2 | 15 | * | (*, *) |
|---|
模型汇总
| 95.81% | 95.29% | 241.87 | 243.23 | 251.43 |
|---|
拟合优度检验
| 偏差 | 45 | 32.28 | 0.922 |
|---|
| Pearson | 45 | 31.93 | 0.929 |
|---|
| Hosmer-Lemeshow | 8 | 7.10 | 0.526 |
|---|
方差分析
| 模型 | 4 | 737.452 | 184.363 | 737.45 | 0.000 |
|---|
| 烘制时间 | 1 | 203.236 | 203.236 | 203.24 | 0.000 |
|---|
| 烘制温度 2 | 1 | 100.432 | 100.432 | 100.43 | 0.000 |
|---|
| 烘制时间*烘制时间 | 1 | 6.770 | 6.770 | 6.77 | 0.009 |
|---|
| 烘制时间*烘制温度 2 | 1 | 80.605 | 80.605 | 80.61 | 0.000 |
|---|
| 误差 | 45 | 32.276 | 0.717 | | |
|---|
| 合计 | 49 | 769.728 | | | |
|---|
以未编码单位表示的回归方程
| P(事件) | = | exp(Y')/(1 + exp(Y')) |
|---|
| Y' | = | -11.984 + 3.361 烘制时间 + 0.08740 烘制温度 2 - 0.0961 烘制时间*烘制时间 - 0.01702 烘制时间*烘制温度 2 |
|---|
异常观测值的拟合和诊断
| 1 | 0.9800 | 0.9376 | 2.0298 | 2.13 | R |
|---|
| 7 | 0.9800 | 0.9396 | 1.9581 | 2.00 | R |
|---|
| 24 | 0.9000 | 0.9497 | -2.0182 | -2.15 | R |
|---|

