请选择您所选的方法或公式。
系数 (Coef)
Minitab 使用最小平方估计值来计算系数。
在矩阵项中,系数的最小平方估计值为:
b = (X'X)-1X'y
有关更高阶次模型系数的更多信息,请参见 Cornell1。
表示法
| 项 | 说明 |
|---|---|
| X | 设计矩阵 |
| y | 响应列 |
- J.J.A. Cornell (1990)。Experiments With Mixtures: Designs, Models, and the Analysis of Mixture Data(混料实验:混料数据的设计、模型和分析),John Wiley & Sons。
系数的标准误(系数标准误)
对于简单线性回归,系数的标准误为:
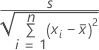
多个回归的系数标准误都是此矩阵的对角线元素的平方根:
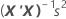
表示法
| 项 | 说明 |
|---|---|
| xi | 第 i 个预测变量值 |
 | 预测变量的平均值 |
| X | 设计矩阵 |
| X' | 设计矩阵的转置 |
| s2 | 均方误 |
T 值
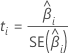
表示法
| 项 | 说明 |
|---|---|
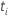 | 检验统计量(对于第  系数) 系数) |
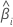 | 第 估计系数 估计系数 |
 | 标准误(对于第 估计系数 估计系数 |
P 值 – 系数表
回归系数等于 0 的原假设的双侧 P 值为:
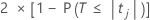
自由度是误差的自由度,如下所示:
n – p
表示法
| 项 | 说明 |
|---|---|
 | t 分布的累积分布函数具有等于误差自由度的自由度。 |
| tj | 第 j 个系数的 t 统计量。 |
| n | 数据集中的观测值个数。 |
| p | 项的自由度总和。 |
方差膨胀因子 (VIF)
可以通过针对其余预测变量回归每个预测变量并对 R2 值求反来获得 VIF。
公式
对于预测变量 xj,VIF 为:

表示法
| 项 | 说明 |
|---|---|
| R2( xj) | 将 xj 的判定系数作为响应变量,将模型中的其他项作为预测变量 |
