方法
Minitab 使用两种方法来分析重复或仿行测量值的标准差:最小二乘法和极大似然法。这两种方法都基于含对数链接函数的线性模型:ln(σ) = Aγ,其中 A 是设计矩阵,γ 是要估计的参数的向量。使用对数链接函数的一个优势是,拟合值始终为正值。
当参数的数量等于数据点的数量时,这两种方法在饱和模型中产生相等的结果。
对于最小二乘估计,Minitab 使用加权的最小二乘回归。如果重复或仿行的数目相同,则权重相等。
对于 MLE,Minitab 会假设原始数据来自正态分布。样本方差的分布与 χ2 分布相关。
设计矩阵
Minitab 使用与一般线性模型 (GLM) 中相同的设计矩阵方法,其使用回归来拟合您指定的模型。首先,Minitab 从您指定的因子和模型创建一个设计矩阵。此矩阵的列(称为 X)表示模型中的项。
设计矩阵包含对应于模型中项的 n 个行(其中 n = 观测值个数)和几个列区组。第一个区组用于常量,只包含一列,一个包含所有值的列。连续因子的区组也只包含一列。类别因子的列区组包含 r 列,其中 r = 因子的自由度。
例如,一个部分因子设计包含 3 个因子,其中每个因子具有 2 个水平。模型包含 3 个主效应。每行的编码如下:
| 区组 | 因子 1 | 因子 2 | 因子 3 |
|---|---|---|---|
| 1 | −1 | −1 | −1 |
| 1 | 1 | −1 | −1 |
| 1 | −1 | 1 | −1 |
| 1 | 1 | 1 | −1 |
| 1 | −1 | −1 | 1 |
| 1 | 1 | −1 | 1 |
| 1 | −1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
效应
为每个因子估计的效应。只会为 2 水平模型计算效应,不会为一般因子模型进行此计算。针对因子效应的公式为:
效应 = 系数 * 2
系数 (Coef)
回归方程中的总体回归系数的估计值。对于每个因子,Minitab 计算 k - 1 个系数,其中 k 是因子中的水平数。对于双因子、2 水平、全因子模型,因子和交互作用的系数公式为:


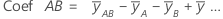
对于此双因子、2 水平、全因子模型,系数的标准误为:

有关包含两个以上因子或其因子具有两个以上水平的模型的信息,请参见 Montgomery1。
表示法
| 项 | 说明 |
|---|---|
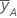 | 因子 A 的高水平处的 y 的均值 |
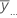 | 所有观测值的总体均值 |
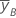 | 因子 B 的高水平处的 y 的均值 |
 | 因子 A 和 B 的高水平处的 y 的均值 |
| MSE | 均方误 |
| n | 估计的项的 - 1 和 1(在协方差矩阵中)的数目 |
加权回归
加权最小二乘回归是处理具有非恒定方差的观测值的方法。如果方差不是恒定的,则观测值应具备以下特点:
- 应当为较大的方差指定相对较小的权重
- 应当为较小的方差指定相对较大的权重
权重反映用于计算每个标准差的重复或仿行的数目。基于较多数据的标准差将获得较高的权重。
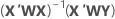
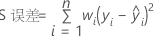
表示法
| 项 | 说明 |
|---|---|
| X | 设计矩阵 |
| x | 转置设计矩阵 |
| w | 对角线上的 n x n 权重矩阵 |
| Y | 对数标准差值的向量 |
| n | 观测值个数 |
| wi | 第 i 个观测值的权重 |
| yi | 第 i 个观测值的对数标准差值 |
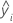 | 第 i 个观测值的对数标准差的拟合值 |
计算权重
您可以基于离散模型(在分析位置模型时使用),通过使用拟合或调整的方差来计算和存储权重。
- 1 / 拟合方差
- σ2(between) + σ2 (within) / 重复数
“Between”和“within”指的是试验的游程。一个游程中的变异是您对重复观测值的标准差的度量。游程之间的变异指新游程的变异的其他来源。
在分析重复之间的标准差时,将模型模型拟合到 s(within)。如果具有仿行,则 Minitab 将结合 σ2 (within) 的模型和仿行之间均值的方差以获得 σ2 (between) 的估计值。然后,σ2 (between) 的估计值与 σ2 (within) / 重复数重新组合,以获得与离散模型一致的均值的方差估计值。
此方法假设 σ2(between) 保持不变,并且不依赖于因子水平。如果此假设不正确,则您可能需要通过使用“预处理”响应(具有 )将模型拟合为 x 的方差,以获取各仿行中的 σ2。
)将模型拟合为 x 的方差,以获取各仿行中的 σ2。
如果您的模型中有协变量,则应在重复的方差中考虑到它们。不能考虑拟合方差中的协变量。
