平方和 (SS)
平方距离和。所给出的公式适用于全因子、双因子(其中包含因子 A 和 B)模型。这些公式可以扩展为具有两个以上因子的模型。有关详细信息,请参见 Montgomery1。
SS 合计是模型中的总变异。SS (A) 和 SS (B) 是估计的因子水平均值(在总体均值周围)的平方差和。SS 误差是残差平方和。它也称为处理内误差。计算如下:



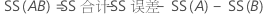

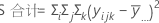
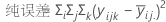
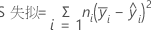
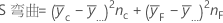


- D.C. Montgomery (1991)。Design and Analysis of Experiments(试验的设计和分析),第三版,John Wiley & Sons。
表示法
| 项 | 说明 |
|---|---|
| a | 因子 A 中的水平数 |
| b | 因子 B 中的水平数 |
| n | 仿行总数 |
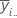 | 因子 A 的第 i 个水平的均值 |
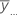 | 所有观测值的总体均值 |
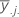 | 因子 B 的第 j 个水平的均值 |
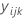 | 分别位于因子 A 的第 i 个水平和因子 B 的第 j 个水平以及第 k 个仿行的观测值 |
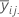 | 因子 A 的第 i 个水平以及因子 B 的第 j 个水平的均值 |
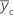 | 中心点的平均响应 |
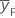 | 因子点的平均响应 |
| nF | 因子点数 |
连续平方和
Minitab 将方差的 SS 回归或处理分量分解为每个因子的连续平方和。连续平方和取决于将因子或预测变量输入到模型中的顺序。在指定以前输入的因子的情况下,连续平方和是 SS 回归中唯一由因子解释的部分。
例如,如果模型有三个因子或预测变量 X1、X2 和 X3,在 X1 已存在于模型中的给定条件下,X2 的连续平方和会显示 X2 解释的其余变异的量。要获得不同的因子序列,请重复分析并以不同的顺序输入因子。
调整的平方和
调整的平方和并不取决于项输入到模型中的顺序。无论项输入到模型中的顺序如何,在模型中指定所有其他项的情况下,调整的平方和都是由项解释的变异量。
例如,如果模型有三个因子 X1、X2 和 X3,在 X1 和 X3 的项也已经位于模型中的情况下,X2 的调整的平方和显示由 X2 的项解释的其余变异量。
三种因子的调整的平方和的计算公式如下:
- SSR(X3 | X1, X2) = SSE (X1, X2) - SSE (X1, X2, X3) 或
- SSR(X3 | X1, X2) = SSR (X1, X2, X3) - SSR (X1, X2)
其中,在模型中给定 X1 和 X2 的情况下,SSR(X3 | X1, X2) 是 X3 的调整的平方和。
- SSR(X2, X3 | X1) = SSE (X1) - SSE (X1, X2, X3) 或
- SSR(X2, X3 | X1) = SSR (X1, X2, X3) - SSR (X1)
其中,在模型中给定 X1 的情况下,SSR(X2, X3 | X1) 是 X2 和 X3 的调整的平方和。
如果模型 1 中有三个以上的因子,则可以扩展这些公式。
- J. Neter、W. Wasserman 和 M.H. Kutner (1985)。Applied Linear Statistical Models(应用线性统计模型),第二版。Irwin, Inc.。
自由度 (DF)
对于包含因子 A 和 B 及区组变量的全因子设计,与每个平方和相关联的自由度数目是:


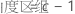

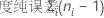


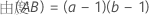
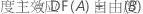
对于具有中心点的双水平设计,弯曲自由度为 1。
表示法
| 项 | 说明 |
|---|---|
| a | 因子 A 中的水平数 |
| b | 因子 B 中的水平数 |
| c | 区组数 |
| n | 观测值总数 |
| ni | 第 i 个因子水平组合的观测值个数 |
| m | 因子水平组合数 |
| p | 系数数目 |
调整 MS – 项

F
一种用于确定交互作用和主效应是否显著的检验。用于模型项的公式是:

检验的自由度为:
- 分子 = 项自由度
- 分母 = 误差自由度
较大的 F 值支持否定没有非显著效应的原假设。
对于平衡裂区设计,针对难以改变的因子的 F 统计量对分母中的整区误差使用 MS。对于其他裂区设计,Minitab 使用 WP 误差和 SP 误差的线性组合来构建基于预期均方的分母。
P 值 – 方差分析表
p 值是从具有如下自由度 (DF) 的 F 分布得出的概率:
- 分子自由度
- 检验中一个或多个项的自由度总和
- 分母自由度
- 误差的自由度
公式
1 − P(F ≤ fj)
表示法
| 项 | 说明 |
|---|---|
| P(F ≤ f) | F 分布的累积分布函数 |
| f | 检验的 f 统计量 |
纯误差失拟检验
- 每组仿行中均值的响应偏差平方和,并将其相加以生成纯误差平方和 (SS PE)。
- 纯误差均方
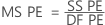

其中 n = 观测值个数,m = 可区分 x 水平组合的数量
- 失拟平方和
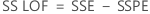
- 失拟均方

- 检验统计量

较大的 F 值和较小的 p 值表明模型不合适。
P 值 – 失拟检验
- 分子自由度
- 失拟自由度
- 分母自由度
- 纯误差自由度
公式
1 − P(F ≤ fj)
表示法
| 项 | 说明 |
|---|---|
| P(F ≤ fj) | F 分布的累积分布函数 |
| fj | 检验的 f 统计量 |
