自由度
总自由度 (DF) 是数据中的信息量。分析使用该信息来估计未知总体参数的值。总自由度由样本中的观测值个数确定。项的自由度显示了项所使用的信息量。增加样本数量可提供有关总体的更多信息,从而增加总自由度。增加模型中项的数量会使用更多信息,这会减少用于估计参数估计值变异性的可用自由度。
- 弯曲的自由度
- 如果设计具有中心点,则一个自由度对应于弯曲检验。如果中心点的项在模型中,则弯曲行是模型的一部分。如果中心点的项不在模型中,则弯曲行是用于检验模型中各项的误差的一部分。
- 误差的自由度
- 如果两个条件都满足,Minitab 会分割与弯曲无关的误差自由度。第一个条件是必须具有能够与当前未包含在模型中的数据拟合的项。例如,如果设计中具有区组,但这些区组不在模型中。中心点项需始终对应于弯曲,所以中心点项不计数为一个项(您可将其与当前未包含在模型中的数据拟合)。
调整平方和
调整的平方和是对模型的不同分量变异的度量。模型中各预测变量的顺序不会影响调整的平方和的计算。在方差分析表中,Minitab 会将平方和分成不同的分量,这些分量描述了不同来源导致的变异。
- 调整平方和模型
- 调整的模型平方和是模型中总平方和与误差平方和之差(与只使用响应均值的模型相比)。这是模型中各项的所有连续平方和的总和。
- 调整平方和项组
- 模型中某一项组的调整平方和是该组中所有项的连续平方和的总和。它可以量化响应数据中由项组解释的变异量。
- 调整平方和项
- 调整的项平方和是与只具有其他项的模型相比,模型平方和的增加。它可以量化响应数据中由模型内每个项解释的变异量。
- 调整平方和误差
- 调整的误差平方和是残差平方和。它可以量化预测变量无法解释的数据中的变异。
- 调整平方和弯曲
- 调整的弯曲平方和可以是模型平方和或误差平方和的一部分。它可以量化响应数据中由中心点项解释的变异量。此变异代表一个或多个二次项的组合效应。
- 调整平方和纯误差
- 调整的纯误差平方和是误差平方和的一部分。当纯误差的自由度存在时,纯误差平方和即存在。有关更多信息,请转到有关自由度 (DF) 的部分。可以量化具有相同的因子、区组和协变量值的观测值数据中的变异量。
- 调整平方和合计
- 调整的总平方和是模型平方和与误差平方和的总和。它可以量化数据中的总变异量。
解释
Minitab 使用调整的平方和来计算方差分析表中的 p 值。Minitab 还使用平方和来计算 R2 统计量。通常,您需解释 p 值和 R2 统计量,而非平方和。
调整的 MS
调整的均方度量一个项或模型解释变异性的程度,从而假定模型中包含所有其他项,而不论其在模型中的顺序如何。与调整的平方和不同,调整的均方要考虑自由度。
调整的均方误(也称为 MSE 或 s2)是围绕拟合值的方差。
解释
Minitab 使用调整的均方来计算方差分析表中的 p 值。Minitab 还使用调整的均方来计算调整的 R2 统计量。通常,您需解释 p 值和调整的 R2 统计量,而非调整的均方。
连续平方和
连续平方和是对模型不同分量的变异的度量。与调整的平方和不同,连续平方和取决于项在模型中的顺序。在方差分析表中,Minitab 会将连续平方和分成不同的分量,这些分量描述了不同来源导致的变异。
- 连续平方和模型
- 模型的连续平方和是总平方和与误差平方和之差。它是模型中各项的所有平方和的总和。
- 连续平方和项组
- 模型中某一项组的连续平方和是该组中所有项的平方和的总和。它可以量化响应数据中由项组解释的变异量。
- 连续平方和项
- 与只具有方差分析表中其上方项的模型相比,项的连续平方和是模型平方和的增加。当项添加到具有其上方项的模型时,它可以量化模型平方和的增加。
- 连续平方和误差
- 连续误差平方和就是残差平方和。它可以量化预测变量无法解释的数据中的变异。
- 连续平方和弯曲
- 弯曲的连续平方和可以是模型平方和或误差平方和的一部分。它可以量化响应数据中由中心点项解释的变异量。此变异代表一个或多个二次项的组合效应。
- 连续平方和纯误差
- 连续纯误差平方和是误差平方和的一部分。当纯误差的自由度存在时,纯误差平方和即存在。有关更多信息,请转到有关自由度 (DF) 的部分。可以量化具有相同的因子、区组和协变量值的观测值数据中的变异量。
- 连续平方和合计
- 连续总平方和是模型平方和与误差平方和的总和。它可以量化数据中的总变异量。
贡献
贡献显示的是方差分析表中每个来源对连续平方总和 (Seq SS) 贡献的百分比。
解释
百分比越高表明来源占响应变异的比例越多。
F 值
在方差分析表中,将显示每个检验的 F 值。
- 模型的 F 值
- 此 F 值是用于确定模型中的任何项是否与响应(包括协变量、区组、因子项和弯曲)相关联的检验统计量。
- 作为组的协变量的 F 值
- 此 F 值是用于确定任何协变量是否同时与响应相关联的检验统计量。
- 单个协变量的 F 值
- 此 F 值是用于确定单个协变量是否与响应相关联的检验统计量。
- 区组的 F 值
- 此 F 值是用于确定区组间的不同条件是否与响应相关联的检验统计量。
- 因子项的类型的 F 值
- 此 F 值是用于确定一组项是否与响应相关联的检验统计量。项组示例包括线性效应和双因子交互作用。
- 单个项的 F 值
- 此 F 值是用于确定项是否与响应相关联的检验统计量。
- 弯曲的 F 值
- 此 F 值是用于确定任何因子与响应是否存在弯曲关系的检验统计量。
- 失拟检验的 F 值
- 此 F 值是用于确定模型是否缺少项(其中包含当前试验中的因子)的检验统计量。如果区组或协变量在逐步过程期间从模型中删除,则失拟检验将同时包括这些项。
解释
Minitab 使用 F 值计算 P 值,使用 P 值可以做出有关检验的统计意义显著性的决定。P 值是一个概率,用来测量否定原假设的证据。概率越低,否定原假设的证据越充分。足够大的 F 值表明统计意义显著。
如果要使用 F 值来确定是否要否定原假设,请将 F 值与临界值进行比较。可以在 Minitab 中计算临界值,也可以在大多数统计书籍的 F 分布表中查找临界值。有关使用 Minitab 计算临界值的更多信息,请转到 使用逆累积分布函数 (ICDF),然后单击“使用 ICDF 计算临界值”。
P 值 – 模型
P 值是一个概率,用来度量否定原假设的证据。概率越低,否定原假设的证据越充分。
解释
要确定模型是否解释响应中的变异,请将模型的 p 值与显著性水平进行比较以评估原假设。模型的原假设声明模型不解释响应中的任何变异。通常,显著性水平(用 α 或 alpha 表示)为 0.05 即可。显著性水平 0.05 指示在模型不解释响应中的变异时得出模型对此进行解释的风险为 5%。
- P 值 ≤ α:模型解释响应中的变异
- 如果 P 值小于或等于显著性水平,则可得出模型解释响应中变异的结论。
- P 值 > α:证据不足,无法得出模型解释响应中变异的结论
- 如果 P 值大于显著性水平,则无法得出模型解释响应中变异的结论。您可能需要拟合新模型。
P 值 – 协变量
P 值是一个概率,用来度量否定原假设的证据。概率越低,否定原假设的证据越充分。
在设计试验中,协变量解释了可度量但难以控制的变量。例如,医院网络的质量团队成员设计一个试验,用于研究接受全膝关节置换手术的患者的住院时间。对于该试验,团队可以控制诸如术前指令格式等因子。为了避免偏差,团队记录了关于其无法控制的协变量的数据,如患者年龄。
解释
要确定响应与协变量之间的关联是否在统计意义上显著,请将该协变量的 P 值与显著性水平进行比较以评估原假设。原假设声明该协变量的系数等于零,这意味着该协变量与响应之间没有关联。
通常,显著性水平(用 α 或 alpha 表示)为 0.05 即可。显著性水平 0.05 指示在游程之间的不同条件不改变响应时得出这些条件改变响应的风险为 5%。
当评估包含协变量的模型中项的统计意义显著性时,请考虑方差膨胀因子 (VIF)。
- P 值 ≤ α:关联在统计意义上显著
- 如果 P 值小于或等于显著性水平,则可以得出响应与协变量之间的关联在统计意义上显著的结论。
- P 值 > α:关联在统计意义上不显著
- 如果 P 值大于显著性水平,则无法得出响应与协变量之间的关联在统计意义上显著的结论。您可能需要拟合无协变量的模型。
注意
在大多数因子设计中,所有 VIF 值为 1,这简化了统计显著性的确定过程。在模型中包含协变量和在数据收集期间进行修补游程是用于增大 VIF 值的两种常用方法,可使统计显著性的解释过程复杂化。VIF 值位于“系数”表中。有关更多信息,请转到分析因子设计的系数表并单击 VIF。
P 值 – 区组
P 值是一个概率,用来度量否定原假设的证据。概率越低,否定原假设的证据越充分。
区组可说明在不同条件下执行的游程之间可能发生的差异。例如,工程师设计一个试验用于研究焊接,并且无法在同一天收集所有数据。焊接质量受多个每天都在变化的变量(如相对湿度)的影响,工程师无法对此进行控制。为了说明这些不可控的变量,工程师将每天执行的游程分组到单独的区组中。区组说明来自不可控变量的变异,使这些效应不会与工程师想要研究的因子的效应相混淆。有关 Minitab 如何为区组指定游程的更多信息,请转到什么是区组?。
解释
要确定游程之间的不同条件是否会更改响应,请将区组的 p 值与显著性水平进行比较以评估原假设。原假设声明不同的条件不会更改响应。
通常,显著性水平(用 α 或 alpha 表示)为 0.05 即可。显著性水平 0.05 指示在游程之间的不同条件不改变响应时得出这些条件改变响应的风险为 5%。
- P 值 ≤ α:不同的条件会更改响应
- 如果 P 值小于或等于显著性水平,则得出不同的条件会更改响应的结论。
- P 值 > α:证据不足,无法得出不同的条件会更改响应的结论
- 如果 P 值大于显著性水平,则无法得出不同的条件会更改响应的结论。您可能需要拟合无区组的模型。
P 值 – 因子、交互作用和项组
P 值是一个概率,用来度量否定原假设的证据。概率越低,否定原假设的证据越充分。
解释
- 如果一个协变量显著,则可以得出该协变量的系数不等于零的结论。
- 如果一个类别因子显著,则可以得出并非所有水平均值都相等的结论。
- 如果一个交互作用项显著,则因子与响应之间的关系取决于该项中的其他因子。
项组检验
如果项组在统计意义上显著,则可以得出结论:组中至少一项在响应上具有效应。当您使用统计显著性来确定要保留在模型中的项时,您通常不会同时删除整个项组。单个项的统计显著性可因为模型中的项而发生改变。
方差分析
| 来源 | 自由度 | Adj SS | Adj MS | F 值 | P 值 |
|---|---|---|---|---|---|
| 模型 | 10 | 447.766 | 44.777 | 17.61 | 0.003 |
| 线性 | 4 | 428.937 | 107.234 | 42.18 | 0.000 |
| 材料 | 1 | 181.151 | 181.151 | 71.25 | 0.000 |
| 注塑压力 | 1 | 112.648 | 112.648 | 44.31 | 0.001 |
| 注塑温度 | 1 | 73.725 | 73.725 | 29.00 | 0.003 |
| 冷却温度 | 1 | 61.412 | 61.412 | 24.15 | 0.004 |
| 2 因子交互作用 | 6 | 18.828 | 3.138 | 1.23 | 0.418 |
| 材料*注塑压力 | 1 | 0.342 | 0.342 | 0.13 | 0.729 |
| 材料*注塑温度 | 1 | 0.778 | 0.778 | 0.31 | 0.604 |
| 材料*冷却温度 | 1 | 4.565 | 4.565 | 1.80 | 0.238 |
| 注塑压力*注塑温度 | 1 | 0.002 | 0.002 | 0.00 | 0.978 |
| 注塑压力*冷却温度 | 1 | 0.039 | 0.039 | 0.02 | 0.906 |
| 注塑温度*冷却温度 | 1 | 13.101 | 13.101 | 5.15 | 0.072 |
| 误差 | 5 | 12.712 | 2.542 | ||
| 合计 | 15 | 460.478 |
在此模型中,针对双因子交互作用的检验在 0.05 水平上不具有统计显著性。此外,针对所有双因子交互作用的检验在统计意义上不显著。
方差分析
| 来源 | 自由度 | Adj SS | Adj MS | F 值 | P 值 |
|---|---|---|---|---|---|
| 模型 | 5 | 442.04 | 88.408 | 47.95 | 0.000 |
| 线性 | 4 | 428.94 | 107.234 | 58.16 | 0.000 |
| 材料 | 1 | 181.15 | 181.151 | 98.24 | 0.000 |
| 注塑压力 | 1 | 112.65 | 112.648 | 61.09 | 0.000 |
| 注塑温度 | 1 | 73.73 | 73.725 | 39.98 | 0.000 |
| 冷却温度 | 1 | 61.41 | 61.412 | 33.31 | 0.000 |
| 2 因子交互作用 | 1 | 13.10 | 13.101 | 7.11 | 0.024 |
| 注塑温度*冷却温度 | 1 | 13.10 | 13.101 | 7.11 | 0.024 |
| 误差 | 10 | 18.44 | 1.844 | ||
| 合计 | 15 | 460.48 |
如果从与具有最高 p 值的双因子交互作用开始一次将模型精简一个项,则最后一个双因子交互作用在 0.05 水平上具有统计显著性。
P 值 – 弯曲
P 值是一个概率,用来度量否定原假设的证据。概率越低,否定原假设的证据越充分。
当设计具有中心点时,Minitab 会检验弯曲。此检验着眼于中心点处相对于预期均值的响应拟合均值(如果模型项和响应之间的关系是线性关系)。要查看弯曲,请使用因子图。
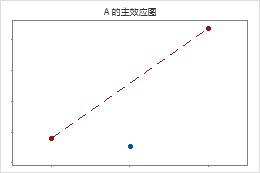
中心点远离用于联接角点均值的线,这表明存在弯曲关系。可使用 p 值来验证弯曲是否在统计意义上显著。
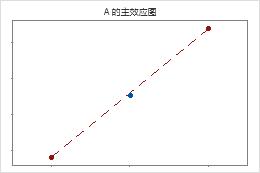
中心点紧邻用于联接角点均值的线。弯曲可能在统计意义上不显著。
解释
要确定是否至少一个因子与响应具有弯曲关系,请将 p 值与显著性水平进行比较以评估原假设。原假设声明因子与响应之间的所有关系都是线性关系。
通常,显著性水平(用 α 或 alpha 表示)为 0.05 即可。显著性水平 0.05 指示在游程之间的不同条件不改变响应时得出这些条件改变响应的风险为 5%。
- P 值 ≤ α:至少有一个因子与响应具有弯曲关系
- 如果 P 值小于或等于显著性水平,则可得出至少有一个因子与响应具有弯曲关系的结论。您可能需要向设计中添加轴点,以便能够对弯曲建模。
- P 值 > α:证据不足,无法得出任何因子与响应具有弯曲关系的结论
- 如果 P 值大于显著性水平,则无法得出任何因子与响应具有弯曲关系的结论。如果弯曲是模型的一部分,则可能需要重新拟合模型(没有中心点的任何项),使得曲线是误差的一部分。
注意
通常,如果弯曲在统计意义上不显著,则可删除中心点项。如果在模型中保留中心点,Minitab 会假设模型中包含无法由因子设计拟合的弯曲。由于拟合程度不够,等值线图、曲面图和重叠等值线图不可用。此外,Minitab 不会在设计的因子水平和响应优化器之间插入值。有关如何使用模型的更多信息,请转到已存储的模型概述。
P 值 – 失拟
P 值是一个概率,用来度量否定原假设的证据。概率越低,否定原假设的证据越充分。
解释
- P 值 ≤ α:失拟在统计意义上显著
- 如果 p 值小于或等于显著性水平,则得出模型未正确指定关系的结论。要改善模型,可能需要添加项或者变换数据。
- P 值 > α:失拟在统计意义上不显著
-
如果 p 值大于显著性水平,则检验不检测任何失拟。
