指数族和链接函数
从经典线性模型扩展到广义线性模型包含两部分:指数族分布和链接函数。
指数族
第一部分会将线性模型扩展到作为大型分布族(称为指数族)成员的响应变量。分布的指数族成员具有已观测响应变量的概率分布函数,这些函数的一般形式为:
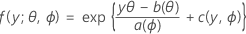
其中,a(∙)、b(∙) 和 c(∙) 依赖于响应变量的分布。参数 θ 是通常称为规范参数的位置参数,ϕ 称为离差参数。函数 a(ϕ) 通常采用 a(ϕ)= ϕ/ ω 形式,其中 ω 是可能因观测值不同而异的已知常量或权重。(在 Minitab 中,当给出权重时,函数 a(ϕ) 会相应地调整。)
指数族的成员可以是离散分布或连续分布。作为指数族成员的连续分布的示例包括正态分布和 Gamma 分布。作为指数族成员的离散分布的示例包括二项分布和 Poisson 分布。下表列出了其中一些分布的特征。
| 分布 | ϕ | b(θ) | a(φ) | c(y, ϕ) |
| 正态 | σ2 | θ2/2 | φω |  |
| 二项 | 1 | 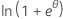 |
φ/ω | -ln(y!) |
| Poisson | 1 | exp(θ) | φ/ω |  |
链接函数
第二部分是链接函数。链接函数将第 i 个观测值中的响应变量的均值与如下形式的线性预测变量相关:
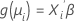
经典线性模型是此一般公式的特殊案例,其中,链接函数是恒等函数。
第二部分中链接函数的选择取决于第一部分的指数族的特定分布。特别是,指数族中的每个分布都有一个叫典范链接函数的特殊链接函数。此链接函数满足方程 g (μi) = Xi'β= θ,其中,θ 是典范参数。典范链接函数会生成一些需要的模型统计属性。可以使用拟合优度统计量比较使用不同链接函数的拟合。使用某些链接函数可能是出于历史原因或因为其在规律方面有特殊意义。例如,Logit 链接函数的优势之一就是它提供优势比的估计值。另一个示例是 Normit 链接函数,它假设存在一个基础变量,该变量遵循具有二元类别的正态分布。
Minitab 提供三种链接函数:Minitab 为每类模型提供三种链接函数。可以使用不同的链接函数确定能够充分拟合各种数据的模型。对于二项模型,链接函数是 Logit、Normit(又称 Probit)和 Gompit(又称互补对数-对数)函数。这些函数是逆累积标准 Logistic 分布函数 (Logit)、逆累积标准正态分布函数 (Normit) 和逆 Gompertz 分布函数 (Gompit)。Logit 函数是二项模型的典范链接函数,因此 Logit 函数是默认的链接函数。
| 模型 | 名称 | 链接函数,g(μi) |
| 二项 | Logit | 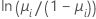 |
| 二项 | Normit (Probit) | 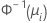 |
| 二项 | Gompit(互补对数 - 对数) |  |
表示法
| 项 | 说明 |
|---|---|
| μi | 第 i 行的均值响应 |
| g(μi) | 链接函数 |
| X | 预测变量的向量 |
| β | 与预测变量相关的系数的向量 |
 | 正态分布的逆累积分布函数 |
因子/协变量模式
描述数据集中的一组因子/协变量值。Minitab 会为每种因子/协变量模式计算事件概率、残差及其他诊断度量标准。
例如,如果数据集包含性别和民族(因子)以及年龄(协变量),则这些预测变量的组合可能包含与对象一样多的不同的协变量模式。如果数据集仅包含民族和性别两个因子,且每个因子有两个编码水平,则仅存在四种可能的因子/协变量模式。如果您将输入的数据作为频率、成功、试验或失效数据,则每行包含一个因子/协变量模式。
设计矩阵
Minitab 使用如一般线性模型 (GLM) 中所用的相同设计矩阵方法,该模型使用回归来拟合指定的模型。首先,Minitab 会根据因子和您指定的模型创建一个设计矩阵。此矩阵的列称为 X,表示模型中的项。
- 常量
- 协变量
- 区组
- 因子
- 交互作用
- 常量
- 协变量
- 连续因子
对于区组,列数比区组数少一个。
2 水平设计中的类别因子和交互作用
在 2 水平设计中,类别因子的项具有一列。任何交互作用项也具有一列。
一般因子设计中的类别因子
| A 的水平 | A1 | A2 | A3 |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 |
| 4 | -1 | -1 | -1 |
一般因子设计中的交互作用
要计算交互作用项的列,需将交互作用项中的因子的对应列相乘。例如,假设因子 A 有 6 个水平,C 有 3 个水平,D 有 4 个水平。那么项 A * C * D 具有 5 x 2 x 3 = 30 列。要获得这些水平,需将 A 的每列乘以 C 的每列和 D 的每列。
裂区设计中的整区列
注意
Minitab 不会分析具有二元响应的裂区设计。
对于裂区设计,Minitab 使用两个设计矩阵版本。一个版本为任何 2 水平因子设计都使用相同的矩阵。另一个矩阵包含表示整区的列区组。例如,整区误差项的计算使用第二个版本的设计矩阵。整区的列在难以改变的因子和(仅涉及难以改变的因子的)交互作用的列之后。
