自由度
总自由度 (DF) 是数据中的信息量。分析使用该信息来估计未知总体参数的值。总 DF 比数据中的行数少 1。项的自由度显示了项所使用的信息量。增加模型中项的数量会向模型中添加更多系数,这会减少用于误差的 DF。误差的 DF 是模型中未使用的剩余自由度。
注意
对于 2 水平因子设计或 Plackett-Burman 设计,如果设计内有中心点,则一个 DF 对应于弯曲检验。如果中心点的项在模型中,则弯曲行是模型的一部分。如果中心点的项不在模型中,则弯曲行是用于检验模型中各项的误差的一部分。在响应曲面和定义筛选设计中,由于可以估计二次项,因此弯曲检验并非必需。
序贯偏差
- 模型
- 回归模型的序贯偏差可以量化由模型解释的总偏差量。
- 项
- 项的序贯偏差可以量化该特定项之前(包括该特定项)的模型和不包含该特定项的模型之间的差值。
- 错误
- 误差的序贯偏差可以量化模型无法解释的偏差。
- 合计
- 总序贯偏差是模型的序贯偏差与误差的序贯偏差之和。总序贯偏差可以量化数据总偏差。
解释
当您指定将序贯偏差用于检验时,Minitab 使用序贯偏差计算回归模型和各项的 P 值。通常情况下,您可以解释 P 值而不是序贯偏差。
贡献
贡献显示方差分析表中每个来源对总序贯偏差贡献的百分比。
解释
较高的百分比表示该来源可以解释响应变量中较多的偏差。回归模型的贡献百分比与偏差 R2 相同。
调整的偏差
调整的偏差可以度量不同模型分量的变异。模型中预测变量的顺序不会影响调整的偏差的计算。在偏差表中,Minitab 将偏差分割成不同的分量,以描述由不同来源解释的偏差。
- 模型
- 回归模型的调整的偏差可以量化当前模型和常量模型之间的差值。
- 项
- 项的调整偏差可以量化包含该项的模型和不包含该项的模型之间的差值。
- 误差
- 误差的调整偏差可以量化模型无法解释的偏差。
- 合计
- 总调整偏差是模型的调整偏差与误差的调整偏差之和。总调整偏差可以量化数据总偏差。
解释
Minitab 使用调整的偏差计算项的 P 值。Minitab 使用调整的偏差计算偏差 R2 统计量。通常情况下,您可以解释 P 值和 R2 统计量,而不是偏差。
调整的均值
调整的均值偏差可度量项或模型为每个自由度解释的偏差量。计算每一项的调整的均值偏差时会假设所有其他项都在模型中。
解释
Minitab 使用卡方值来计算项的 p 值。通常情况下,您可以解释 p 值而不是调整的均方。
卡方
方差分析表中的每一项都具有一个卡方值。卡方值是检验统计量,可以确定项或模型是否与响应变量相关。
解释
Minitab 使用卡方统计量计算 P 值,使用 P 值可以做出有关项和模型的统计显著性的决定。P 值是一个概率,用来测量否定原假设的证据。概率越低,否定原假设的证据越充分。足够大的卡方统计量产生的 P 值较小,这表示项或模型在统计意义上显著。
P 值 – 模型
P 值是一个概率,用来度量否定原假设的证据。概率越低,否定原假设的证据越充分。
解释
- P 值 ≤ α:至少一个系数不同于 0
- 如果 p 值小于或等于显著性水平,则得出至少有一个系数不同于 0 的结论。
- P 值 > α:证据不足,无法得出至少一个系数不同于 0 的结论
- 如果 p 值大于显著性水平,则无法得出至少有一个系数不同于 0 的结论。
偏差表中的检验为似然比检验。系数表的扩展显示中的检验为 Wald 近似检验。与 Wald 近似检验相比,较小样本的似然比更准确。
P 值 – 项
P 值是一个概率,用来测量否定原假设的证据。概率越低,否定原假设的证据越充分。
解释
- P 值 ≤ α:关联在统计意义上显著
- 如果 P 值小于或等于显著性水平,则可以得出响应变量与项之间的关联在统计意义上显著的结论。
- P 值 > α:关联在统计意义上不显著
- 如果 p 值大于显著性水平,则无法得出响应变量与该项之间的关联在统计意义上显著的结论。您可能希望重新拟合没有该项的模型。
- 如果一个连续因子显著,则可以得出该因子的系数不是零的结论。
- 如果一个类别因子显著,则可以得出并非所有因子水平都具有相同事件概率的结论。
- 如果一个交互作用项显著,则可以得出因子与事件概率之间的关系取决于该项中其他因子的结论。
- 如果一个二次项在统计意义上显著,则可以得出结论:响应曲面中具有弯曲。
方差分析表中的检验是似然比检验。系数表的扩展显示中的检验为 Wald 近似检验。较小样本的似然比与 Wald 近似检验更准确。
P 值 – 弯曲
P 值是一个概率,用来度量否定原假设的证据。概率越低,否定原假设的证据越充分。
当设计具有中心点时,Minitab 会检验弯曲。此检验着眼于中心点处相对于预期均值的响应拟合均值(如果模型项和响应之间的关系是线性关系)。要查看弯曲,请使用因子图。
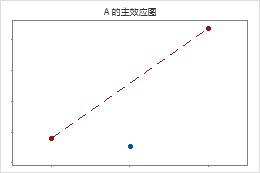
中心点远离用于联接角点均值的线,这表明存在弯曲关系。可使用 p 值来验证弯曲是否在统计意义上显著。
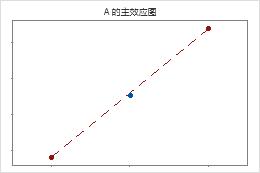
中心点紧邻用于联接角点均值的线。弯曲可能在统计意义上不显著。
解释
要确定是否至少一个因子与响应具有弯曲关系,请将 p 值与显著性水平进行比较以评估原假设。原假设声明因子与响应之间的所有关系都是线性关系。
通常,显著性水平(用 α 或 alpha 表示)为 0.05 即可。显著性水平 0.05 指示在游程之间的不同条件不改变响应时得出这些条件改变响应的风险为 5%。
- P 值 ≤ α:至少有一个因子与响应具有弯曲关系
- 如果 P 值小于或等于显著性水平,则可得出至少有一个因子与响应具有弯曲关系的结论。您可能需要向设计中添加轴点,以便能够对弯曲建模。
- P 值 > α:证据不足,无法得出任何因子与响应具有弯曲关系的结论
- 如果 P 值大于显著性水平,则无法得出任何因子与响应具有弯曲关系的结论。如果弯曲是模型的一部分,则可能需要重新拟合模型(没有中心点的任何项),使得曲线是误差的一部分。
注意
通常,如果弯曲在统计意义上不显著,则可删除中心点项。如果在模型中保留中心点,Minitab 会假设模型中包含无法由因子设计拟合的弯曲。由于拟合程度不够,等值线图、曲面图和重叠等值线图不可用。此外,Minitab 不会在设计的因子水平和响应优化器之间插入值。有关如何使用模型的更多信息,请转到已存储的模型概述。
