什么是多元方差分析(方差的多变量分析)?
多元方差分析是同时分析多个响应变量和一个共同预测变量集之间关系的检验。与方差分析一样,多元方差分析需要连续响应变量和类别预测变量。与运行多个方差分析(一次一个响应变量)相比,多元方差分析具有多个重要优势。
- 增加功效
- 您可以使用响应变量之间的数据协方差结构,来同时检验均值的相等性。如果响应变量彼此相关,则此附加信息有助于检测太小而无法通过单个方差分析来检测的差异。
- 检测多变量响应模式
- 因子可能影响响应之间的关系,而不会影响单个响应。方差分析不会检测这些多变量形式,如下方数字所示。
- 控制全族误差率
- 错误否定原假设的概率可能会随着每个连续方差分析增加。运行一个多元方差分析来同时检验所有响应变量可以使全族误差率与您的 alpha 水平相等。
例如,您正在研究不同合金(1、2 和 3)对公司所制造产品的强度和可塑性的影响。您首先执行了两个独立的方差分析,但结果均不显著。对于这种出人意料的结果,您使用单值图绘制了这两个响应变量的原始数据。这些图直观地确认了不显著的方差分析结果。
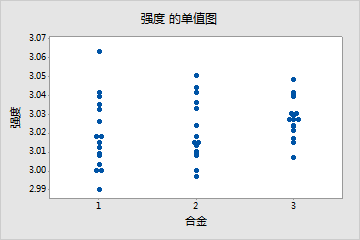
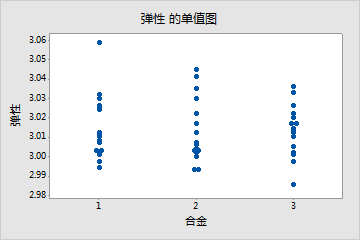
由于这些响应变量彼此相关,因此您执行了一次多元方差分析。这一次,结果很显著,p 值小于 0.05。为了更好地理解结果,您创建了一个散点图。
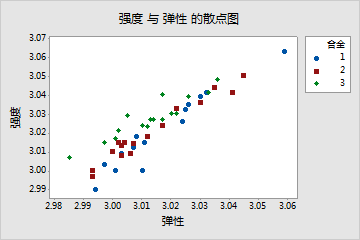
单值图从单变量的角度显示,合金不会显著影响强度或可塑性。但是,相同数据的散点图却显示,不同合金会改变这两个响应变量之间的关系。也就是说,对于特定的可塑性分值,合金 3 通常比合金 1 和 2 的强度分值高。
注意
通常,您应在进行任何分析前首先绘制数据图,因为这样做有助于确定哪种方法更合适。
多元方差分析中包含哪个多变量检验?
Minitab 针对模型中的每项以及特殊请求项自动执行四种多变量检验:
- Wilk 检验
- Lawley-Hotelling 检验
- Pillai 检验
- Roy 最大根检验
上述四种检验都以两个 SSCP(平方和和叉积)矩阵为基础:
- 与每项相关联的 H(假设)矩阵;也称为样本平方和之间的矩阵
- 与检验误差相关联的 E(误差)矩阵;也称为样本平方和之内的矩阵
请求假设时,系统将显示 SSCP 矩阵。
您可以将检验统计量表示为 H、E 或 H 和 E,或者表示为 E-1 H 的特征值。您可以请求显示这些特征值。(如果存在重复特征值,则对应的特征向量不是唯一的。在此情况下,Minitab 显示的特征向量和手册中或其他软件中的特征向量可能不一致。但是多元方差分析检验始终唯一。)
