什么是协变量?
协变量通常用于方差分析和 DOE。在这些模型中,协变量为任意连续变量,通常在数据收集期间不可控制。包含协变量的模型可让您包含并调整在试验中已度量但非随机化或不可控的输入变量。添加协变量可以在很大程度上提高模型的准确度,并可能显著影响最终的分析结果。在模型中包含协变量可以减少模型中的误差,从而提高因子检验的功效。常见的协变量包括环境温度、湿度以及对部件或对象采取处理手段之前的特征。
例如,一位工程师希望研究四类铁条的腐蚀水平。该工程师让每种铁条接触一种液体处理方式,从而加速腐蚀效果,但他无法控制液体的温度。温度就是应在模型中考虑的协变量。
在 DOE 中,某工程师可能对协变量环境温度对于两种不同油漆的干燥时间的效应感兴趣。
向一般线性模型添加协变量的示例
某纺织公司使用三种不同的机器生产单丝纤维。他们想要确定使用不同机器产生的纤维抗断强度是否不同。他们从每台机器中随机选择 5 种纤维,收集其强度和直径数据。因为纤维强度与其直径相关,所以他们还记录了纤维直径,作为可能的协变量来使用。
| C1 | C2 | C3 |
|---|---|---|
| 机器 | 直径 | 强度 |
| 1 | 20 | 36 |
| 1 | 25 | 41 |
| 1 | 24 | 39 |
| 1 | 25 | 42 |
| 1 | 32 | 49 |
| 2 | 22 | 40 |
| 2 | 28 | 48 |
| 2 | 22 | 39 |
| 2 | 30 | 45 |
| 2 | 28 | 44 |
| 3 | 21 | 35 |
| 3 | 23 | 37 |
| 3 | 26 | 42 |
| 3 | 21 | 34 |
| 3 | 15 | 32 |
- 确认协变量和响应是否线性相关。 您可以通过在 Minitab 中使用拟合线图分析数据来执行此操作。
- 选择。
- 在 响应(Y) 中,输入强度。
- 在 预测变量(X) 中,输入直径。
- 评估数据位置与拟合线的接近程度以及 R2 接近“完美拟合” (100%) 的程度。
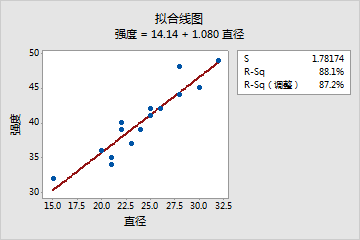
拟合线图表明直径和强度之间存在很强的线性关系 (87.2%)。
- 执行含有协变量的 GLM 分析。
- 选择。
- 在响应中,输入强度。
- 在因子中,输入机器。
- 在协变量中,输入直径。
- 单击确定。
对于纤维生产数据,Minitab 显示如下结果:
一般线性模型: 强度 与 直径, 机器
方差分析 来源 自由度 Adj SS Adj MS F 值 P 值 直径 1 178.014 178.014 69.97 0.000 机器 2 13.284 6.642 2.61 0.118 误差 11 27.986 2.544 失拟 7 18.486 2.641 1.11 0.487 纯误差 4 9.500 2.375 合计 14 346.400机器的 F 统计量为 2.61,p 值为 0.118。因为 p 值 >0.05,您无法否定“在 5% 的显著性水平下,所以纤维强度不会根据所使用的机器而有所不同”的原假设。您可以假设所有机器的纤维强度都相同。请注意,直径(协变量)的 F 统计量为 69.97,p 值为 0.000。这表明,协变量效应显著。也就是说,直径对于纤维强度具有统计意义非常显著的影响。
现在,假设您重新运行分析并忽略协变量。这将得出以下输出:
一般线性模型: 强度 与 机器
方差分析 来源 自由度 Adj SS Adj MS F 值 P 值 机器 2 140.4 70.20 4.09 0.044 误差 12 206.0 17.17 合计 14 346.4请注意,F 统计量为 4.09,p 值为 0.044。模型中没有协变量,您会在 5% 显著性水平下否定原假设,并得出纤维强度会根据使用的机器而有所不同的结论。
此结论与您在执行协变量分析时得到的结论完全相反。该示例表明无法包含协变量可能生成误导性分析结果的程度有多严重。
