请选择您所选的方法或公式。
Minitab 提供了在单因子方差分析中比较多因子均值的五种不同方法:Tukey 法、Fisher 法、Dunnett 法、许氏 MCB 法和 Games-Howell 法。这些检验的公式列举如下。
表示法
| 项 | 说明 |
|---|---|
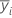 | 第 i 个因子水平的样本均值 |
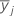 | 第 j 个因子水平的样本均值 |
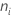 | 水平 i 中的观测值个数 |
| r | 水平数 |
| s | 合并标准差或 sqrt(MSE) |
| u | 误差的自由度 |
| α | 产生类型 I 错误的整体概率 |
| α* | 产生类型 I 错误的单个概率 |
Tukey:
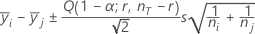
其中 Q = t 化范围分布的 α 百分位数上限,具有 r 和 nT - r 自由度。
要从整体误差率中查找个别误差率,请使用下列公式:

Fisher:
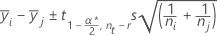
其中 t = 学生 t 分布 α/2 点的上限,具有 u df。
要从个别误差率中查找整体置信水平,请使用下列公式:
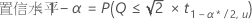
Dunnett:

要了解如何计算 d,请参考许氏1 中的第 63 页。
许氏 MCB 法:
我们会按实例提供公式,其中所有组大小均等于 n。不均等组大小的公式可在许氏1 中找到。假设您选择了最佳值作为最大均值,现在希望用第 i 个均值减去其他值中的最大值得到置信区间。
下端点小于零,且

上端点大于零,且

要了解如何计算 d,请参考许氏1 中的第 83 页。
当最佳值为最小水平均值时,公式相同,最大值替换为最小值的情况除外。
Games-Howell 和 Welch 检验
Welch 检验统计量的计算方法如下。
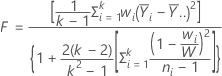
Welch 检验的 p 值是分子自由度为 k - 1 的 F 分布的上尾概率,其中 k 是 X 水平数,而分母自由度通过以下公式得出:
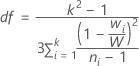
μi - μj 的比较区间为
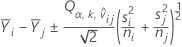
临界值基于 k 组的 t 化范围 (Q),与 Tukey-Kramer 区间相似。但对于 Games-Howell 法,Minitab 将针对每个比较计算不同的自由度:
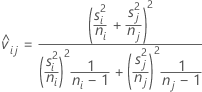
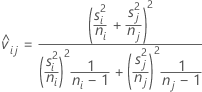
用于计算调整的 P 值的 T 比等于:
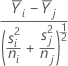
其中:
类别因子的第 i 个水平的第 j 个响应等于:Yij,j = 1, ... , ni;i = 1, ... k
处于第 i 个水平的平均响应等于:
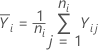
样本方差等于:
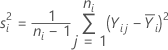
水平 i 的权重等于:
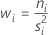
所有权重的总和等于:
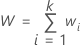
整体加权平均响应等于:
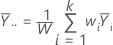
致谢
我们非常感谢 Jason C. Hsu 先生帮助我们设计和实施多重比较。
[1] J.C. Hsu (1996)。Multiple Comparisons, Theory and methods(多重比较,理论和方法)。Chapman & Hall。
