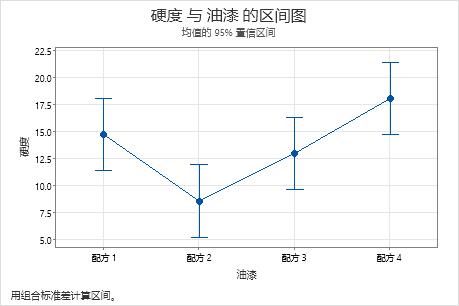
某化学工程师想要比较四种油漆混料的硬度。每种油漆混料取六份样品涂到一小块金属上,待金属块凝固后再测量每种样品的硬度。为了检验均值是否相等,并评估均值对之间的差分,分析师配合使用单因子方差分析和多重比较。
- 打开样本数据,喷漆硬度.MWX。
- 选择。
- 选择所有因子水平的响应数据位于同一列中。
- 在响应中,输入硬度。
- 在因子中,输入油漆。
- 单击比较按钮,然后选择Tukey。
- 在每个对话框中单击确定。
解释结果
油漆硬度方差分析得到的 p 值小于 0.05。此结果表明油漆混料的硬度明显不同。工程师了解到部分组均值不相同。
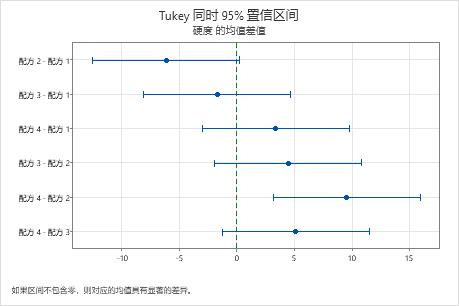
工程师使用 Tukey 比较结果正式检验一对组之间的差分在统计意义上是否显著。包含 Tukey 整体置信区间的图形显示,混料 2 和混料 4 的均值之间差分的置信区间为 (3.114, 15.886)。此范围不包含零,表明这些均值之间的差分显著。工程师可以使用此差分估计值来确定差分在实际意义上是否显著。
其余均值对的置信区间都包括零,表明这些差分并不显著。
低预测值 R2 (24.32%) 表明模型针对新观测值生成的预测值不准确。这种不准确性可能是由于组的数量较小引起的。因此,工程师不应使用该模型进行样本数据之外的广义化。
方法
| 原假设 | 所有均值都相等 |
|---|
| 备择假设 | 并非所有的均值都相等 |
|---|
| 显著性水平 | α = 0.05 |
|---|
因子信息
| 油漆 | 4 | 配方 1, 配方 2, 配方 3, 配方 4 |
|---|
方差分析
| 油漆 | 3 | 281.7 | 93.90 | 6.02 | 0.004 |
|---|
| 误差 | 20 | 312.1 | 15.60 | | |
|---|
| 合计 | 23 | 593.8 | | | |
|---|
模型汇总
| 3.95012 | 47.44% | 39.56% | 24.32% |
均值
| 配方 1 | 6 | 14.73 | 3.36 | (11.37, 18.10) |
|---|
| 配方 2 | 6 | 8.57 | 5.50 | (5.20, 11.93) |
|---|
| 配方 3 | 6 | 12.98 | 3.73 | (9.62, 16.35) |
|---|
| 配方 4 | 6 | 18.07 | 2.64 | (14.70, 21.43) |
|---|
使用 Tukey 方法和 95% 置信度对信息进行分组
| 配方 4 | 6 | 18.07 | A | |
|---|
| 配方 1 | 6 | 14.73 | A | B |
|---|
| 配方 3 | 6 | 12.98 | A | B |
|---|
| 配方 2 | 6 | 8.57 | | B |
|---|