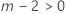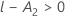F 统计量的分母自由度的计算和 F 统计量的计算有所不同。对于给定的 F 统计量，两种方法的分子自由度的计算和 p 值的确定过程都相同。
Kenward-Roger 近似
Kenward-Roger 近似是一种用于检验固定效应项的统计显著性的方法。
F 统计量
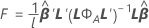
其中
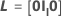
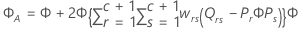
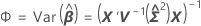
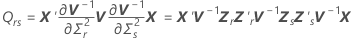
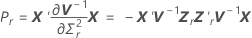
表示法
项
说明
l
分子自由度，即要检验的项中的参数个数
0
具有 0 个分量的矩阵
Il
具有维度 l 的恒等矩阵
c + 1
方差分量数
wrs
以下项的渐近方差-协方差矩阵的第 (r, s) 个分量
V−1
方差-协方差矩阵的逆矩阵
有关该表示法的更多详细信息，请转到“方法”部分。
分母自由度
其中
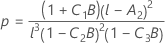
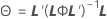
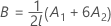
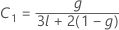
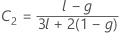
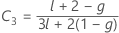
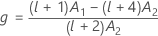
Kenward-Roger λ
Kenward-Roger λ 的值取决于两个条件。
如果两个条件都成立，则公式如下：
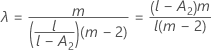
如果任一条件成立，则 λ = 1。
在原假设下，当自由度为 DF Num 和 DF Den 时，lambda × F 服从渐进 F 分布。P 值的计算中使用此属性。
Satterthwaite 近似
Satterthwaite 近似是一种用于检验固定效应项的统计显著性的方法。
F 统计量
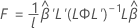
其中，L 和 的定义与 Kenward-Roger 近似中的定义相同。
分母自由度
用于确定自由度的过程包括多个步骤。
对固定效应参数向量估计值的方差执行频谱分解：
其中，P 是正交特征向量矩阵，而 D 是对角特征向量矩阵，两者都具有 l × l 维度。
将 lr 定义为 P'L, r = 1, ..., l 的第 r 行，并且设
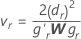其中，dr 是 D 的第 r 个对角元素，而 W 是渐近方差-协方差矩阵（对于），并且 gr 是以下元素的梯度向量：
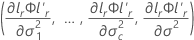
其中
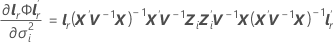
i = 1, …, c，并且
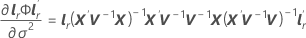
设
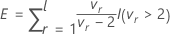
其中，是指示函数，用于排除符合以下条件的项
分母自由度取决于 E 的值。
如果 E > l，则自由度如下：
否则，DF Den = 1
分子自由度 (DF Num)
固定效应的自由度取决于效应的类型。
效应
自由度
固定因子
协变量
1
包含固定因子的交互作用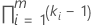
表示法
项
说明
k
固定因子项中的水平数
m
交互作用中的因子数
P 值 – 固定效应检验
P 值根据以下表达式进行计算：
表示法
项
说明
自由度分别等于分子自由度和分母自由度的 F 分布的累积分布函数
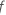为某项计算的 F 值
1 Kenward, M.G. 和 Roger, J. H. (1997)。Small Sample Inference for Fixed Effects from Restricted Maximum Likelihood（根据受限极大似然的小样本固定效应推断）。生物统计学，第 53 卷，第 3 期，第 983 至 997 页。
2 Giesbrecht, F.G. 和 Burns, J. C. (1985)。Two-Stage Analysis Based on a Mixed Model: Large-Sample Approximation Theory and Small-Sample Simulation Results（基于混合模型的两阶段分析：大样本近似理论和小样本模拟结果），生物计量学，第 41 卷，第 2 期，第 477 至 486 页。
3 Fai, A. H. 和 Cornelius, P. L. (1996) Approximate F-Tests of Multiple Degree of Freedom Hypotheses in Generalized Least Squares Analyses of Unbalanced Split-Plot Experiments（不平衡裂区试验的广义最小二乘分析中多重自由度假设的近似 F 检验），统计计算模拟杂志，第 54 卷，第 363 至 378 页
的定义与 Kenward-Roger 近似中的定义相同。
其中，dr 是 D 的第 r 个对角元素，而 W 是渐近方差-协方差矩阵（对于
），并且 gr 是以下元素的梯度向量：
是指示函数，用于排除符合以下条件的项
