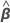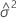请选择您所选的方法或公式。
混合效应模型和对数似然
混合效应模型的一般形式
混合效应模型包含固定效应和随机效应。混合效应模型的一般形式为:
y = Xβ + Z1μ1+ Z2μ2 + ... + Zcμc + ε
表示法
| 项 | 说明 |
|---|---|
| y | 响应值的 n x 1 向量 |
| X | 固定效应项的 n x p 设计矩阵,p ≤ n |
| β | 未知参数的 p x 1 向量 |
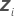 | n x mi 设计矩阵(用于模型中的第 随机项) 随机项) |
| μi | 独立变量的 mi x 1 向量(独立变量来自 N(0,  ) ) |
| ε | 独立变量的 n x 1 向量(独立变量来自 N(0,  ) ) |
| n | 观测值个数 |
| p | 参数个数( 中) 中) |
| c | 模型中的随机项数 |
方差-协方差矩阵
根据用于混合效应模型的一般形式的模型假定,响应向量 y 具有多元正态分布,该分布包含均值向量 Xβ 和以下方差-协方差矩阵:
V(σ2) = V(σ2, σ21, ... , σ2c) = σ2In + σ21Z1Z'1 + ... + σ2cZcZ'c
其中
σ2 = (σ2, σ21, ... , σ2c)'
σ2, σ21, ... , σ2c 称为方差分量。
通过分解方差,您可以在计算混合效应模型的对数似然时找到 H(θ) 的表示形式。
V(σ2) = σ2H(θ) = σ2[In + θ1Z1Z'1 + ... + θcZcZ'c]
表示法
| 项 | 说明 |
|---|---|
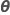 | 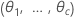 |
| θi | 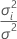 ,第 ,第  随机项的方差与误差方差的比值 随机项的方差与误差方差的比值 |
对数似然
当模型包含随机因子时,默认情况下,通过对受限对数似然函数的相反数进行两次最小化可得出未知参数估计值。求最小值相当于最大化受限对数似然函数。Minitab 使用迭代算法对受限对数似然函数进行最小化。要实现最小化的函数为:




表示法
| 项 | 说明 |
|---|---|
| H | In + θ1Z1Z'1 + ... + θcZcZ'c |
| |H| | H 的行列式 |
| H-1 | 逆 H |
| mi | 水平数(关于第 随机项 随机项 |
 | 误差方差分量 |
| In | 具有 n 个行和列的恒等矩阵 |
受限极大似然 (REML) 估计值
默认情况下,Minitab 计算参数估计值,用于对受限似然函数进行最大化,这相当于对以下函数进行最小化:
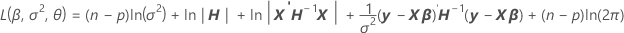
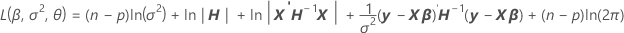
要对函数进行最小化,Minitab 根据 β、σ2 和 θi 为函数实现差异化,并且将以下差值设为等于 0:
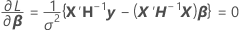
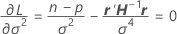
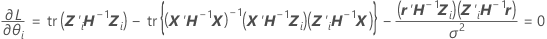
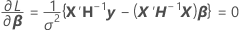
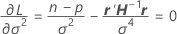
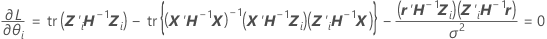
其中,
用于就差异化对估计的参数求解而对前两个方程进行代数重排后,可给出以下方程:
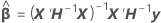
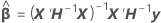

导数(关于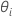 )无法针对以下项而显式解出
)无法针对以下项而显式解出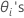 。Minitab 使用 Newton 方法来估计
。Minitab 使用 Newton 方法来估计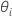 ,步骤如下:
,步骤如下:
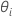 )无法针对以下项而显式解出
)无法针对以下项而显式解出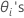 。Minitab 使用 Newton 方法来估计
。Minitab 使用 Newton 方法来估计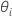 ,步骤如下:
,步骤如下:
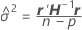
收敛的解(对于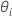 )为方差比值估计值。第
)为方差比值估计值。第 随机项的方差分量如下所示:
随机项的方差分量如下所示:

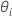 )为方差比值估计值。第
)为方差比值估计值。第 随机项的方差分量如下所示:
随机项的方差分量如下所示:

表示法
| 项 | 说明 |
|---|---|
| tr(·) | 矩阵跟踪 |
| X' | X 的转置 |
1 Rao, C.R. (1971 a)。Estimation of variance covariance components - MINQUE theory(方差协方差分量估计 - MINQUE 理论)。Journal of Multivariate Analysis(多元分析杂志),第 1 期,第 257 至 275 页。
2 Rao, C.R. (1971 b)。Minimum variance quadratic unbiased estimation of variance components(方差分量的最小方差二次无偏估计),Journal of Multivariate Analysis(多元分析杂志),第 1 期,第 445 至 456 页。