研究人员检验四块随机选择的田地上六种紫花苜蓿的产量。为每块田地记录一种紫花苜蓿的产量。
研究人员希望了解紫花苜蓿的品种是否会影响平均产量。该研究人员具有四块可以从中收集数据的田地。但是,研究人员希望可以对不在试验中的田地内紫花苜蓿的生长方式进行建模。因此,研究人员使紫花苜蓿生长所在的田地成为随机因子。研究人员使用混合效应模型来同时评估固定效应和随机效应。
- 打开样本数据紫花苜蓿.MWX。
- 选择。
- 在响应中,输入产量。
- 在随机因子(必需)中,输入田地。
- 在固定因子中,输入品种。
- 单击图形。
- 在图中的残差中,选择条件标准化。
- 在残差图中,选择四合一。
- 在每个对话框中单击确定。
解释结果
在方差分量表中,田地的 p 值为 0.124。假设检验未显示方差分量不为 0 的证据。误差的方差分量的 p 值为 0.003。因为 p 值小于显著性水平 0.05,所以研究人员可以得出误差的方差分量不为 0 的结论。
固定因子项“品种”的 p 值大约为 0 时,就表明至少一种紫花苜蓿对产量的效应与其他五种类型的效应显著不同。
主效应的系数代表每个水平均值和总体均值之间的差值。例如,与品种 1 相关的紫花苜蓿产量大约比总体均值高 0.385 个单位。此系数的 p 值大约为 0 时,就表明品种 1 对产量的效应与“品种”项的另一个水平效应显著不同。为了确定哪些水平效应在统计意义上相同以及哪些水平效应在统计意义上不同,研究人员计划对项执行多重比较分析。
R2 值表明,模型大约解释产量中 92% 的变异。R-sq(调整)值也较高,值大约为 90.2%。研究人员使用此值比较具有不同预测变量数量的模型。
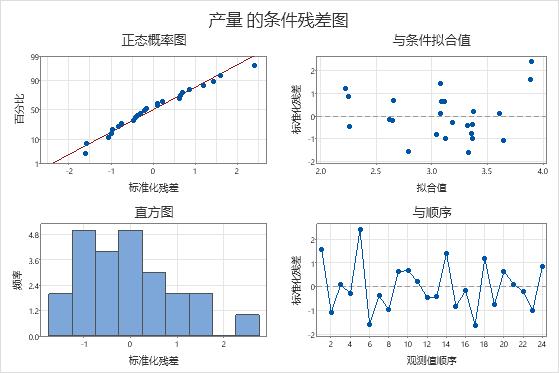
观测值 1 和 5 是异常观测值,因为它们具有大于 2 的标准化残差。研究人员检查数据以确保这些观测值具有正确的响应值。
正态概率图上的残差大致为一条直线,并且这些点在残差与拟合值图上看似随机散布在 0 周围。
方法
| 方差估计 | 带约束的极大似然 |
|---|---|
| 固定效应的自由度 | Kenward-Roger |
因子信息
| 因子 | 类型 | 水平数 | 值 |
|---|---|---|---|
| 田地 | 随机 | 4 | 1, 2, 3, 4 |
| 品种 | 固定 | 6 | 1, 2, 3, 4, 5, 6 |
方差分量
| 来源 | 变量 | 总和的 % | 变量标准误 | Z 值 | P 值 |
|---|---|---|---|---|---|
| 田地 | 0.077919 | 72.93% | 0.067580 | 1.152996 | 0.124 |
| 误差 | 0.028924 | 27.07% | 0.010562 | 2.738613 | 0.003 |
| 合计 | 0.106843 |
固定效应检验
| 项 | 分子自由度 | 分母自由度 | F 值 | P 值 |
|---|---|---|---|---|
| 品种 | 5.00 | 15.00 | 26.29 | 0.000 |
模型汇总
| S | R-sq | R-sq(调整) | AICc | BIC |
|---|---|---|---|---|
| 0.170071 | 92.33% | 90.20% | 12.54 | 13.52 |
系数
| 项 | 系数 | 系数标准误 | 自由度 | T 值 | P 值 |
|---|---|---|---|---|---|
| 常量 | 3.094583 | 0.143822 | 3.00 | 21.516692 | 0.000 |
| 品种 | |||||
| 1 | 0.385417 | 0.077626 | 15.00 | 4.965016 | 0.000 |
| 2 | 0.145417 | 0.077626 | 15.00 | 1.873287 | 0.081 |
| 3 | 0.107917 | 0.077626 | 15.00 | 1.390205 | 0.185 |
| 4 | -0.319583 | 0.077626 | 15.00 | -4.116938 | 0.001 |
| 5 | 0.395417 | 0.077626 | 15.00 | 5.093838 | 0.000 |
异常观测值的边际拟合和诊断
| 观测值 | 产量 | 拟合值 | 残差 | 标准化残差 | |
|---|---|---|---|---|---|
| 1 | 4.100000 | 3.480000 | 0.620000 | 2.190221 | R |
| 5 | 4.220000 | 3.490000 | 0.730000 | 2.578808 | R |
异常观测值的条件拟合和诊断
| 观测值 | 产量 | 拟合值 | 残差 | 标准化残差 | |
|---|---|---|---|---|---|
| 5 | 4.220000 | 3.895339 | 0.324661 | 2.400733 | R |