Wilk 检验
检验统计量 Wilk lambda 为:
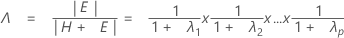
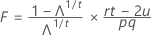
具有 pq 和 (rt – 2u) df。
表示法
| 项 | 说明 |
|---|---|
| H | 假设矩阵 |
| E | 误差矩阵 |
| p | 响应数 |
| q | 假设的 df |
| v 时 | E 的 df |
| s | 最小 (p, q) |
| m | .5 ( | p – q | – 1) |
| n | .5 (v – p – 1) |
| r | v – ..5 (p – q + 1) |
| u | 0.25(pq – 2) |
| t | = Sqrt ([p2 q2 - 4] / p2 + q2 - 5, if p2 + q2 - 5 > 0 |
| t | 1 |
使 λ1≥λ2≥λ3≥ . . . ≥λp 作为 (E** - 1) * H 的特征值。前三个检验统计量可用 H 和 E 或这些特征值来表示。
H 矩阵是在每个 p 变量的对角线上包含“组间”平方和的 p x p 矩阵。H 矩阵计算方法如下:

E 矩阵是包含每个 p 变量的对角线上“组内”平方和的 p x p 矩阵。E 矩阵计算方法如下:
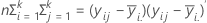
在最初三个检验中,如果 s = 1 或 2,则 F 统计量为确切值;否则为近似值。Minitab 会指出检验何时为近似。
Lawley-Hotelling 检验
检验统计量 Lawley-Hotelling 跟踪为:
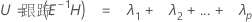
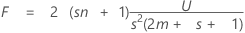
具有 s (2m + s + 1) 和 2 (sn + 1) df。
表示法
| 项 | 说明 |
|---|---|
| H | 假设矩阵 |
| E | 误差矩阵 |
| p | 响应数 |
| q | 假设的 df |
| vv | E 的 df |
| s | 最小 (p, q) |
| m | .5 ( | p – q | – 1) |
| n | .5 (v – p – 1) |
| r | v – 0.5 (p – q + 1) |
| u | 0.25(pq – 2) |
| t | = Sqrt ([p2 q2 - 4] / p2 + q2 - 5, if p2 + q2 - 5 > 0 |
| t | 1 |
使 λ1≥λ2≥λ3≥ . . . ≥λp 成为 (E** - 1) * H 的特征值。前三个检验统计量可以用 H 和 E 或这些特征值来表示。
H 矩阵是在每个 p 变量的对角线上包含“组间” 平方和的 p x p 矩阵。H 矩阵计算方法如下:

E 矩阵是包含每个 p 变量的对角线上“组内”平方和的 p x p 矩阵。E 矩阵计算方法如下:
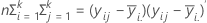
在最初三个检验中,如果 s = 1 或 2,则 F 统计量为确切值;否则为近似值。Minitab 会指出检验何时为近似。
Pillai 检验
检验统计量 Pillai 跟踪为:
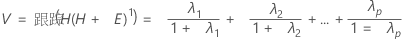

表示法
| 项 | 说明 |
|---|---|
| H | 假设矩阵 |
| E | 误差矩阵 |
| p | 响应数 |
| q | 假设的 df |
| vv | E 的 df |
| s | 最小 (p, q) |
| m | .5 ( | p – q | – 1) |
| n | .5 (v – p – 1) |
| r | v – 0.5 (p – q + 1) |
| u | 0.25(pq – 2) |
| t | = Sqrt ([p2 q2 - 4] / p2 + q2 - 5, if p2 + q2 - 5 > 0 |
| t | 1 |
设 λ1≥λ2≥λ3≥ . . . ≥λp 是 (E** - 1) * H 的特征值。前三个检验统计量可以用 H 和 E 或者这些特征值来表示。
H 矩阵是在每个 p 变量的对角线上包含“组间”平方和的 p x p 矩阵。H 矩阵计算方法如下:

E 矩阵是包含每个 p 变量的对角线上“组内”平方和的 p x p 矩阵。E 矩阵计算方法如下:
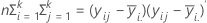
在前三个检验中,如果 s = 1 或 2,则 F 统计量为确切值;否则为近似值。Minitab 会指出什么时候检验为近似。
Roy 的最大根检验
最大特征值,λ1。要完成检验,您必须使用名为 Heck 图的特殊图表,以及参数 s、m 和 n,以查找显著性水平。
查看这些图表的 Heck1。
表示法
| 项 | 说明 |
|---|---|
| s | 最小 (p, q) |
| m | .5 ( | p – q | – 1) |
| n | .5 (v – p – 1) |
使 λ1≥λ2≥λ3≥ . . . ≥λp 成为 (E** - 1) * H 的特征值。前三个检验统计量可用 H 和 E 或这些特征值来表示。
- D.L. Heck (1960),“Charts of Some Upper Percentage Points of the Distribution of the Largest Characteristic Root”(最大特征根分布的部分上百分点图表),The Annals of Statistics(统计学年刊),第 625–642 页。
