均值
均值表显示了基于一个或多个类别变量的组中观测值的拟合均值。拟合均值使用最小二乘来预测平衡设计的平均响应值。
解释
拟合均值估计一个因子的不同水平下的平均响应,并同时求其他因子的平均水平。
使用“均值”表可理解数据中因子水平之间的统计显著性差异。每组的均值都提供了每个总体均值的估计值。请查找统计意义显著的项组均值之间的差异。
对于主效应,该表显示每个因子内的组及其均值。对于交互作用项效应,该表显示组的所有可能的组合。如果交互作用项在统计意义上显著,则在不考虑交互作用效应的情况下,不解释主效应。
在这些结果中,均值表显示均值可用性和质量评分如何根据方法、设备以及方法*设备交互作用项而变化。方法和交互作用项在 0.10 水平时统计意义显著。该表显示方法 1 和方法 2 分别与均值可用性评分 4.819 和 6.212 相关。这些均值之间的差值大于质量评分的相应均值之间的差值。这确认了特征值分析的解释。
但是,因为方法*设备交互作用项的统计意义也显著,所以不考虑交互作用效应就无法解释主效应。例如,交互作用项表显示,使用方法 1,设备 C 与最高可用性评分和最低质量评分相关。但是,使用方法 2,设备 A 与最高可用性评分和约等于最高质量评分的质量评分相关。
响应的最小二乘均值
| 可用性评级 | 质量评级 | |||
|---|---|---|---|---|
| 均值 | 均值标准误 | 均值 | 均值标准误 | |
| 方法 | ||||
| 方法 1 | 4.819 | 0.165 | 5.242 | 0.193 |
| 方法 2 | 6.212 | 0.179 | 6.026 | 0.211 |
| 工厂 | ||||
| 工厂 A | 5.708 | 0.192 | 5.833 | 0.226 |
| 工厂 B | 5.493 | 0.232 | 5.914 | 0.273 |
| 工厂 C | 5.345 | 0.206 | 5.155 | 0.242 |
| 方法*工厂 | ||||
| 方法 1 工厂 A | 4.667 | 0.272 | 5.417 | 0.319 |
| 方法 1 工厂 B | 4.700 | 0.298 | 5.400 | 0.350 |
| 方法 1 工厂 C | 5.091 | 0.284 | 4.909 | 0.334 |
| 方法 2 工厂 A | 6.750 | 0.272 | 6.250 | 0.319 |
| 方法 2 工厂 B | 6.286 | 0.356 | 6.429 | 0.418 |
| 方法 2 工厂 C | 5.600 | 0.298 | 5.400 | 0.350 |
均值标准误
如果反复从同一总体提取样本,则均值标准误 (SE Mean) 会估计您将获取的拟合均值的变异性。
例如,根据 312 个交货时间的随机样本,得到平均交货时间为 3.80 天,标准差为 1.43 天。这些数字产生的均值标准误为 0.08 天(1.43 除以 312 的平方根)。如果从相同总体中抽取数量相同的多个随机样本,则这些不同样本均值的标准差大约为 0.08 天。
解释
使用均值的标准误可以确定拟合均值对总体均值的估计精确度。
均值标准误的值越小,表明总体均值的估计值越精确。通常,标准差越大,均值的标准误就越大,总体均值的估计值越不精确。样本数量越大,均值的标准误就越小,总体均值的估计值越精确。
均值(协变量)
协变量均值是数据的平均值,即所有观测值之和除以观测值的个数。均值使用表示数据中心的单个值来汇总样本值。
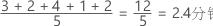
解释
使用均值来描述具有表示数据中心的单个值的协变量。
标准差 (StDev)
标准差是离差的最常用度量,即数据围绕均值扩散的程度。符号 σ(西格玛)常用来表示总体的标准差。符号 s 用来表示样本的标准差。
解释
- 约 68% 的值属于一个均值标准差。
- 95% 的值属于两个标准差。
- 99.7% 的值属于三个标准差。
一个组的样本标准差是该组总体标准差的估计值。标准差用于计算置信区间和 p 值。样本标准差越大,置信区间的精确度越低(越宽),统计功效也越低。
方差分析假定所有水平的总体标准差相等。如果无法假定等方差,请使用 Welch 方差分析,这是一个用于单因子方差分析的选项,在 Minitab 统计软件中可用。
