平方和 (SS)
在矩阵项中,以下是针对不同平方和的公式:
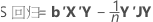


Minitab 同时采用连续平方和与调整的平方和,将 SS 回归或 SS 处理分量分解为由每个项解释的变异量。
表示法
| 项 | 说明 |
|---|---|
| b | 系数向量 |
| X | 设计矩阵 |
| Y | 响应值向量 |
| n | 观测值个数 |
| J | 1s 的 n by n 矩阵 |
连续平方和
Minitab 将方差的 SS 回归或处理分量分解为每个因子的连续平方和。连续平方和取决于将因子或预测变量输入到模型中的顺序。在指定以前输入的因子的情况下,连续平方和是 SS 回归中唯一由因子解释的部分。
例如,如果模型有三个因子或预测变量 X1、X2 和 X3,在 X1 已存在于模型中的给定条件下,X2 的连续平方和会显示 X2 解释的其余变异的量。要获得不同的因子序列,请重复分析并以不同的顺序输入因子。
调整的平方和
调整的平方和并不取决于项输入到模型中的顺序。无论项输入到模型中的顺序如何,在模型中指定所有其他项的情况下,调整的平方和都是由项解释的变异量。
例如,如果模型有三个因子 X1、X2 和 X3,在 X1 和 X3 的项也已经位于模型中的情况下,X2 的调整的平方和显示由 X2 的项解释的其余变异量。
三种因子的调整的平方和的计算公式如下:
- SSR(X3 | X1, X2) = SSE (X1, X2) - SSE (X1, X2, X3) 或
- SSR(X3 | X1, X2) = SSR (X1, X2, X3) - SSR (X1, X2)
其中,在模型中给定 X1 和 X2 的情况下,SSR(X3 | X1, X2) 是 X3 的调整的平方和。
- SSR(X2, X3 | X1) = SSE (X1) - SSE (X1, X2, X3) 或
- SSR(X2, X3 | X1) = SSR (X1, X2, X3) - SSR (X1)
其中,在模型中给定 X1 的情况下,SSR(X2, X3 | X1) 是 X2 和 X3 的调整的平方和。
如果模型 1 中有三个以上的因子,则可以扩展这些公式。
- J. Neter、W. Wasserman 和 M.H. Kutner (1985)。Applied Linear Statistical Models(应用线性统计模型),第二版。Irwin, Inc.。
自由度 (DF)
模型的每个分量的自由度为:
| 变异源 | 自由度 |
|---|---|
| 因子 | ki – 1 |
| 协变量和协变量之间的交互作用 | 1 |
| 包含因子的交互作用 | 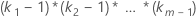 |
| 回归 | p |
| 误差 | n – p – 1 |
| 合计 | n – 1 |
- 数据包含具有相同预测变量值的多个观测值。
- 数据包含用于估计模型中不存在的其他项的正确点。
表示法
| 项 | 说明 |
|---|---|
| ki | 第 i 个因子中的水平数 |
| m | 因子数 |
| n | 观测值个数 |
| p | 模型中的系数数量,不包括常量 |
调整 MS – 回归
回归均方 (MS) 的公式如下:

表示法
| 项 | 说明 |
|---|---|
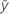 | 平均响应 |
 | 第 i 个拟合响应 |
| p | 模型中的项数 |
Adj MS – 误差
均方误(也称为 MS 误差或 MSE,表示为 s2)是围绕拟合回归线的方差。公式如下:

表示法
| 项 | 说明 |
|---|---|
| yi | 第 i 个观测响应值 |
 | 第 i 个拟合响应 |
| n | 观测值个数 |
| p | 模型中的系数数量,不包括常量 |
F
如果模型中所有因子都是固定的,那么 F 统计量的计算就取决于假设检验的内容,如下所示:
- F(项)
-

- F(失拟)
-

如果模型中具有随机因子,则针对每个项使用期望均方来构建 F。有关更多信息,请参见 Neter 等人的文章1。
表示法
| 项 | 说明 |
|---|---|
| 调整的 MS 项 | 在说明模型中的其他项后,针对项解释的变异量的度量。 |
| MS 误差 | 针对模型不解释的变异的度量。 |
| MS 失拟 | 针对可以通过向模型添加更多项来进行建模的响应中变异的度量。 |
| MS 纯误差 | 针对仿行响应数据中变异的度量。 |
- J. Neter、W. Wasserman 和 M.H. Kutner (1985)。Applied Linear Statistical Models(适用的线性统计模型),第二版。Irwin, Inc.
P 值 – 方差分析表
p 值是从具有如下自由度 (DF) 的 F 分布得出的概率:
- 分子自由度
- 检验中一个或多个项的自由度总和
- 分母自由度
- 误差的自由度
公式
1 − P(F ≤ fj)
表示法
| 项 | 说明 |
|---|---|
| P(F ≤ f) | F 分布的累积分布函数 |
| f | 检验的 f 统计量 |
纯误差失拟检验
- 每组仿行中均值的响应偏差平方和,并将其相加以生成纯误差平方和 (SS PE)。
- 纯误差均方
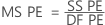

其中 n = 观测值个数,m = 可区分 x 水平组合的数量
- 失拟平方和
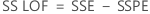
- 失拟均方

- 检验统计量

较大的 F 值和较小的 p 值表明模型不合适。
P 值 – 失拟检验
- 分子自由度
- 失拟自由度
- 分母自由度
- 纯误差自由度
公式
1 − P(F ≤ fj)
表示法
| 项 | 说明 |
|---|---|
| P(F ≤ fj) | F 分布的累积分布函数 |
| fj | 检验的 f 统计量 |
