平衡方差分析的方法和公式

平衡方差分析模型

针对三个或更多因子的平衡方差分析模型是双因子方差分析模型的简单扩展。

具有因子 A、B 和 C 的三因子平衡方差分析模型：

y_ijkm = μ + α _i+ β _j+ γ _k + (αβ)_ij+ (αγ)_ik+ (βγ)_jk+ (αβγ)_ijk+ε_ijkm

如果因子是固定的，则 Σα_i = 0、Σβ_j = 0、Σγ_k = 0、Σ(αβ)_ij = 0、Σ(αγ)_ik = 0、Σ(βγ)_jk = 0、Σ(αβγ)_ijk = 0 和 ε_ijkm 都是独立的 N(0, σ²)。

如果因子是随机的，则 α _i、β _j、γ_k、(αβ)_ij、(αγ)_ik、(βγ)_jk、(αβγ)_ijk 和 ε_ijkm 都是独立随机变量。这些变量属于正态分布，均值为零，且方差由以下公式给定：V(α_i) = σ²_α、V(β _j) = σ²_β、V(γ_k) = σ²_γ、V[(αβ)_ij] = σ²_αβ、V[(αγ)_jk] = σ²_αγ、V[(βγ)_jk] = σ²_βγ、V(ε_ijkm) = σ²。

三因子模型可以扩展为具有三个以上因子的模型。

因子均值

公式

处于指定水平的因子的平均观测值。公式如下：

因子 A 的均值：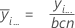

因子 B 的均值：

因子 C 的均值：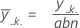

总体均值：

表示法

项	说明
y_i...	A 的第 i 个因子水平的所有观测值总和
y_.j..	B 的第 j 个因子水平的所有观测值总和
y_..k.	C 的第 k 个因子水平的所有观测值的总和
y_....	样本中所有观测值的总和
a	A 中的水平数
b	B 中的水平数
c	C 中的水平数
n	因子和水平的每个组合中的观测值数

平方和 (SS)

平方距离和。SS 合计是数据的总变异。SS (A)、SS (B) 和 SS (C) 是围绕总体均值的估计因子水平均值的变异量。它们也称为处理之间的平方和。SS(AB)、SS(AC)、SS(BC) 和 SS(ABC) 表示各个交互作用项解释的变异量。SS 误差表示拟合值与实际观测值之间的变异量。也称为处理内误差。这些公式假设完全模型已拟合。计算如下：

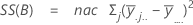
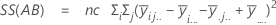
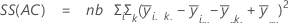
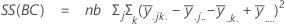
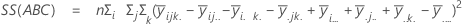
SS 误差 = SS 合计 - SS（对于模型中的所有项）

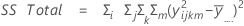
表示法

项	说明
a	因子 A 中的水平数
b	因子 B 中的水平数
c	因子 C 中的水平数
n	试验总数
	因子 A 的第 i 个因子水平的均值
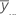	所有观测值的总体均值
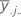	因子 B 的第 j 个因子水平的均值
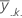	因子 C 的第 k 个因子水平的均值
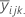	估计的处理均值

自由度 (DF)

模型的每个分量的自由度为：

变异源	自由度
因子	k_i – 1
协变量和协变量之间的交互作用项	1
包含因子的交互作用项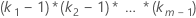
回归	p
Error	n – p – 1
合计	n – 1

表示法

项	说明
k_i	第 i 个因子的水平数
m	因子数
n	观测值个数
p	模型中的系数，不包括常量

均方 (MS)

公式

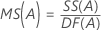
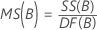
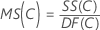
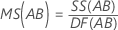
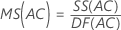
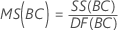
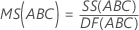
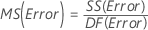
F

针对用于所有固定因子的三因子方差分析，当模型为完全模型时，这些公式为 F 统计量。

公式

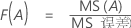
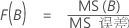
对于 F(A)，分子自由度为 - 1 且分母自由度为 (n - 1)abc。
对于 F(B)，分子自由度为 b - 1 且分母自由度为 (n - 1)abc。
对于 F(C)，分子自由度为 c - 1 且分母自由度为 (n - 1)abc。
对于 F(AB)，分子自由度为 (a - 1)(b - 1) 且分母自由度为 (n - 1)abc。
对于 F(AC)，分子自由度为 (a - 1)(c - 1) 且分母自由度为 (n - 1)abc。
对于 F(BC)，分子自由度为 (b - 1)(c - 1) 且分母自由度为 (n - 1)abc。
对于 F(ABC)，分子自由度为 (a - 1)(b - 1)(c - 1) 且分母自由度为 (n - 1)abc。

如果模型中具有随机因子，则针对每个项使用期望均方来确定每个项的 F 比率。

较大的 F 值支持否定原假设。您可以得出效应统计意义显著的结论。

P 值 – 方差分析表

p 值是从具有如下自由度 (DF) 的 F 分布得出的概率：

分子自由度: 检验中一个或多个项的自由度总和
分母自由度: 误差的自由度

公式

1 − P(F ≤ f_j)

表示法

项	说明
P(F ≤ f)	F 分布的累积分布函数
f	检验的 f 统计量

S

表示法

项	说明
MSE	均方误

R-sq

R² 也称为确定系数。

公式

表示法

项	说明
y_i	第 i 个观测响应值
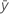	平均响应
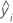	第 i 个拟合响应

R-Sq（调整）

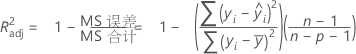
当调整的 R² 计算可以产生负值时，Minitab 会针对这些情况显示零。

表示法

项	说明
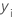	第 i 个观测响应值
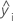	第 i 个拟合响应
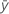	平均响应
n	观测值个数
p	模型中的项数

方差分量

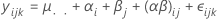
Minitab 仅计算随机因子的方差分量。具有两个随机因子的模型用于代表公式。

其中，α_i, β_j、(αβ)_ij 和 ε_ijk 是独立随机变量。这些变量为正态分布，均值为零，其方差由以下公式给定：

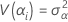
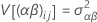
这些方差属于方差分量。在此例中，检验方差分量等于零的假设。

对于具有两个因子的约束混合模型，该模型为：

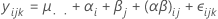
其中 α_i 是固定效应，β_j 是随机效应，(αβ)_ij 是随机效应，ε_ijk 是随机误差。Σα_i = 0 且针对每个 j，Σ(αβ)_ij = 0。方差为 V(β_j) = σ²_β，V[(αβ)_ij] =[(a - 1)/a]σ²_αβ，V(ε_ijk) = σ²。σ²_β、σ²_αβ 以及 σ² 为方差分量。根据固定因子对交互作用分量的求和等于零，这表明此为约束混合模型。

对于具有固定因子 A 和随机因子 B 的无约束混合模型，以下公式可描述该模型：

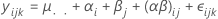
其中，α_i 是固定效应，β_j、(αβ)_ij 和 ε_ijk 是具有零均值和以下方差的不相关随机变量：

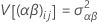
这些方差属于方差分量。Σα _i = 0 且针对每个 j，Σ(αβ)_ij = 0。

此信息用于平衡模型。有关不平衡模型或更多复杂模型的信息，请查看 Montgomery¹ 和 Neter²。

D.C. Montgomery (1991)。Design and Analysis of Experiments（试验的设计和分析），第三版，John Wiley & Sons。
J. Neter、W. Wasserman 和 M.H. Kutner (1985)。Applied Linear Statistical Models（应用的线性统计模型），第二版，Irwin, Inc.。

期望均方

用于具有两个因子 A 和 B 的随机效应模型的期望均方的公式如下：

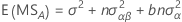
用于具有两个因子 A（固定）和 B（随机）的约束混合效应模型的期望均方的公式如下：

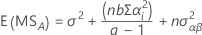
用于具有一个固定因子 A 和一个随机因子 B 的无约束混合模型的期望均方的公式如下：

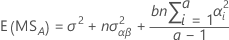
有关计算期望均方的一般规则，以及不平衡模型或更多复杂模型的信息，请查看 Montgomery¹ 和 Neter²。

D.C. Montgomery (1991)。Design and Analysis of Experiments（试验的设计和分析），第三版，John Wiley & Sons.
J. Neter、W. Wasserman 和 M.H. Kutner (1985)。Applied Linear Statistical Models（应用的线性统计模型），第二版，Irwin, Inc.。

表示法

项	说明
b	因子 B 中的水平数
a	因子 A 中的水平数
n	观测值个数
σ²	模型的估计方差
	A 的估计方差
	B 的估计方差
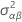	AB 的估计方差
	A 的固定效应

具有随机因子的模型的 F 统计量

如何计算方差分析输出中的 F 统计量

每个 F 统计量都是均方比率。分子是项的均方。已选择分母，以便分子均方预期值仅在相关效应下不同于分母均方预期值。随机项的效应由项的方差分量表示。固定项的效应通过与该项相关的模型分量的平方和除以其自由度表示。因此，高 F 统计量表明效应显著。

当模型中的所有项均固定时，每个 F 统计量的分母都为均方误 (MSE)。但是，对于包含随机项的模型，MSE 并不总是正确的均方。预期均方 (EMS) 可用于确定哪一个适合分母。

示例

假设您执行一个固定因子为“屏幕”，随机因子为“技术”的方差分析，则 EMS 输出如下：

来源	每项的期望均方
(1) 屏幕	(4) + 2.0000(3) + Q[1]
(2) 技术	(4) + 2.0000(3) + 4.0000(2)
(3) 屏幕*技术	(4) + 2.0000(3)
(4) 误差	(4)

带括号的数字表示在源数字旁边列出的与项相关的随机效应。(2) 表示 Tech 的随机效应，(3) 表示 Screen*Tech 交互作用项的随机效应，(4) 表示误差的随机效应。误差的 EMS 是误差项的效应。此外，Screen*Tech 的 EMS 是误差项的效应与 Screen*Tech 双倍的交互作用项效应相加。

要计算“屏幕*技术”的 F 统计量，使用“屏幕*技术”的均方除以误差的均方，使得分子的预期值（“屏幕*技术”的 EMS = (4) + 2.0000(3)）与分母的预期值（误差的 EMS = (4)）仅在交互作用项 (2.0000(3)）上存在差异。因此，高 F 统计量表明“屏幕*技术”交互作用显著。

Q[ ] 的数字表明与源数字旁边列出的项相关的固定效应。例如，Q[1] 是 Screen 的固定效应。Screen 的 EMS 是误差项的效应与两倍的 Screen*Tech 交互作用项效应相加。Q[1] 等于 (b*n * 总和 ((Screen 的水平系数)**2)) 除以 (a - 1)，其中 a 和 b 分别是 Screen 和 Tech 的水平数，n 是仿行数。

要计算 Screen 的 F 统计量，可以使用 Screen 的均方除以 Screen*Tech 的均方，这样，分子的预期值（Screen*Tech 的 EMS = (4) + 2.0000(3) + Q[1]）与分母的预期值（Screen*Tech 的 EMS = (4) + 2.0000(3)）仅在 Screen (Q[1]) 上存在差异。因此，高 F 统计量表明 Screen 效应显著。

为什么我的方差分析输出中在方差分析表的 p 值旁有一个“x”，且带有标签“不是精确的 F 检验”？

针对某个项的精确 F 检验是分子均方的预期值与分母均方的预期值仅在目标项的方差分量或固定因子上有所差异的检验。

但有时，这种均方是无法计算的。在这种情况下，Minitab 会使用一个适当的均方进行近似 F 检验，并在 p 值旁显示“x”，以标识 F 检验不精确。

例如，假设您执行一个固定因子为“补充”，随机因子为“湖”的方差分析，则预期均方 (EMS) 输出如下：

来源	每项的期望均方
(1) 补充	(4) + 1.7500(3) + Q[1]
(2) 湖	(4) + 1.7143(3) + 5.1429(2)
(3) 补充*湖	(4) + 1.7500(3)
(4) 误差	(4)

“补充”的 F 统计量是用补充的均方除以“补充*湖”交互作用项的均方。如果“补充”的效应较小，分子的预期值将等于分母的预期值。下面是精确的 F 检验的示例。

但是请注意，对于非常小的“湖”效应，不存在分子预期值等于分母预期值的均方。因此，Minitab 使用近似 F 检验。在此示例中，“湖”的均方除以“补充*湖”交互作用项的均方。如果“湖”效应较小，这会导致分子预期值约等于分母预期值。

关于“F 检验的分母为零或未定义”消息

Minitab 将显示一条错误消息：出于以下原因之一，F 检验的分母为零或未定义：

不存在至少一个误差自由度。
调整的 MS 值非常小，因此不够精确，无法显示 F 值和 p 值。作为计算方法，请将响应值列乘以 10。然后执行相同的回归模型，但取而代之，针对响应值使用新的响应值列。

注意
响应值乘以 10 将不会影响 Minitab 显示输出的 F 值和 p 值。但是，其余输出中的小数点位置将受到影响，特别是连续平方和、Adj SS、Adj MS、拟合、拟合的标准误和残差列。

如何计算方差分析输出中的 F 统计量

每个 F 统计量都是均方比率。分子是项的均方。已选择分母，以便分子均方预期值仅在相关效应下不同于分母均方预期值。随机项的效应由项的方差分量表示。固定项的效应通过与该项相关的模型分量的平方和除以其自由度表示。因此，高 F 统计量表明效应显著。

当模型中的所有项均固定时，每个 F 统计量的分母都为均方误 (MSE)。但是，对于包含随机项的模型，MSE 并不总是正确的均方。预期均方 (EMS) 可用于确定哪一个适合分母。

示例

假设您执行一个固定因子为“屏幕”，随机因子为“技术”的方差分析，则 EMS 输出如下：

来源	每项的期望均方
(1) 屏幕	(4) + 2.0000(3) + Q[1]
(2) 技术	(4) + 2.0000(3) + 4.0000(2)
(3) 屏幕*技术	(4) + 2.0000(3)
(4) 误差	(4)

带括号的数字表示在源数字旁边列出的与项相关的随机效应。(2) 表示 Tech 的随机效应，(3) 表示 Screen*Tech 交互作用项的随机效应，(4) 表示误差的随机效应。误差的 EMS 是误差项的效应。此外，Screen*Tech 的 EMS 是误差项的效应与 Screen*Tech 双倍的交互作用项效应相加。

要计算“屏幕*技术”的 F 统计量，使用“屏幕*技术”的均方除以误差的均方，使得分子的预期值（“屏幕*技术”的 EMS = (4) + 2.0000(3)）与分母的预期值（误差的 EMS = (4)）仅在交互作用项 (2.0000(3)）上存在差异。因此，高 F 统计量表明“屏幕*技术”交互作用显著。

Q[ ] 的数字表明与源数字旁边列出的项相关的固定效应。例如，Q[1] 是 Screen 的固定效应。Screen 的 EMS 是误差项的效应与两倍的 Screen*Tech 交互作用项效应相加。Q[1] 等于 (b*n * 总和 ((Screen 的水平系数)**2)) 除以 (a - 1)，其中 a 和 b 分别是 Screen 和 Tech 的水平数，n 是仿行数。

要计算 Screen 的 F 统计量，可以使用 Screen 的均方除以 Screen*Tech 的均方，这样，分子的预期值（Screen*Tech 的 EMS = (4) + 2.0000(3) + Q[1]）与分母的预期值（Screen*Tech 的 EMS = (4) + 2.0000(3)）仅在 Screen (Q[1]) 上存在差异。因此，高 F 统计量表明 Screen 效应显著。

为什么我的方差分析输出中在方差分析表的 p 值旁有一个“x”，且带有标签“不是精确的 F 检验”？

针对某个项的精确 F 检验是分子均方的预期值与分母均方的预期值仅在目标项的方差分量或固定因子上有所差异的检验。

但有时，这种均方是无法计算的。在这种情况下，Minitab 会使用一个适当的均方进行近似 F 检验，并在 p 值旁显示“x”，以标识 F 检验不精确。

例如，假设您执行一个固定因子为“补充”，随机因子为“湖”的方差分析，则预期均方 (EMS) 输出如下：

来源	每项的期望均方
(1) 补充	(4) + 1.7500(3) + Q[1]
(2) 湖	(4) + 1.7143(3) + 5.1429(2)
(3) 补充*湖	(4) + 1.7500(3)
(4) 误差	(4)

“补充”的 F 统计量是用补充的均方除以“补充*湖”交互作用项的均方。如果“补充”的效应较小，分子的预期值将等于分母的预期值。下面是精确的 F 检验的示例。

但是请注意，对于非常小的“湖”效应，不存在分子预期值等于分母预期值的均方。因此，Minitab 使用近似 F 检验。在此示例中，“湖”的均方除以“补充*湖”交互作用项的均方。如果“湖”效应较小，这会导致分子预期值约等于分母预期值。

关于“F 检验的分母为零或未定义”消息

Minitab 将显示一条错误消息：出于以下原因之一，F 检验的分母为零或未定义：

不存在至少一个误差自由度。
调整的 MS 值非常小，因此不够精确，无法显示 F 值和 p 值。作为计算方法，请将响应值列乘以 10。然后执行相同的回归模型，但取而代之，针对响应值使用新的响应值列。

注意
响应值乘以 10 将不会影响 Minitab 显示输出的 F 值和 p 值。但是，其余输出中的小数点位置将受到影响，特别是连续平方和、Adj SS、Adj MS、拟合、拟合的标准误和残差列。

拟合值

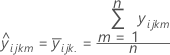
表示法

对于三因子模型：

项	说明
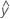	因子 A 的第 i 个水平、因子 B 的第 j 个水平和因子 C 的第 k 个水平下的观测拟合值
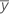	因子 A 的第 i 个水平、因子 B 的第 j 个水平和因子 C 的第 k 个水平下的观测值的均值
n	因子 A 的第 i 个水平、因子 B 的第 j 个水平和因子 C 的第 k 个水平下的观测值数

残差 (Resid)

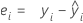
表示法

项	说明
e_i	第 i 个残差
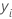	第 i 个观测响应值
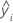	第 i 个拟合响应

平衡方差分析 的方法和公式

关于本主题

平衡方差分析模型

因子均值

公式

表示法

平方和 (SS)

表示法

自由度 (DF)

表示法

均方 (MS)

公式

F

公式

P 值 – 方差分析表

公式

表示法

S

表示法

R-sq

公式

表示法

R-Sq（调整）

表示法

方差分量

期望均方

表示法

具有随机因子的模型的 F 统计量

如何计算方差分析输出中的 F 统计量

示例

为什么我的方差分析输出中在方差分析表的 p 值旁有一个“x”，且带有标签“不是精确的 F 检验”？

关于“F 检验的分母为零或未定义”消息

注意

如何计算方差分析输出中的 F 统计量

示例

为什么我的方差分析输出中在方差分析表的 p 值旁有一个“x”，且带有标签“不是精确的 F 检验”？

关于“F 检验的分母为零或未定义”消息

注意

拟合值

表示法

残差 (Resid)

表示法

平衡方差分析的方法和公式