方法
对于双因子模型,均值分析是确定交互效应是否显著或主效应是否不同于总平均值的过程。对于双因子均值分析,数据必须是平衡的。
均值
公式
处于指定水平的因子的平均观测值。Minitab 在图形中绘制每个因子水平的均值。
| 因子 A 的第 i 个水平的均值: |
 |
| 因子 B 的第 j 个水平的均值: |
 |
表示法
| 项 | 说明 |
|---|---|
| yi. | 因子 A 的第 i 个水平的所有观测值总和 |
| y.j. | 因子 B 的第 j 个水平的所有观测值的总和 |
| a | A 中的水平数 |
| b | B 中的水平数 |
| n | 分别位于因子 A 的第 i 个水平和因子 B 的第 j 个水平的案例数 |
总平均值(中心线)
公式
样本中所有观测值的平均值。Minitab 在主效应的图形上使用总平均值作为中心线。

表示法
| 项 | 说明 |
|---|---|
| y... | 样本中所有观测值的总和 |
| a | A 中的水平数 |
| b | B 中的水平数 |
| n | 分别位于因子 A 的第 i 个水平和因子 B 的第 j 个水平的案例数 |
主效应的决策上限和下限
决策限表明因子水平均值与总均值是否不同。决策上限 (UDL) 或决策下限 (LDL) 之外的点与总均值在统计意义上不同。
决策上限和下限的计算基于因子中的水平数和每个水平的观测值数而有所不同。以下公式显示因子 A 的决策上限和下限。要计算因子 B 的决策限,请将特定于因子 A 的项替换为因子 B 的等效项。
双水平因子
因子 A 的决策上限和下限为:
- UDLA =
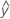 ...+ (.5) * hα* Sqrt[(MSE) * (2 / n1)]
...+ (.5) * hα* Sqrt[(MSE) * (2 / n1)] - LDLA =
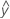 ...- (.5) * hα* Sqrt[(MSE) * (2 / n1)]
...- (.5) * hα* Sqrt[(MSE) * (2 / n1)]
其中,ha = 绝对值 (t(a / 2; abn - ab),MSE = 均方误 (来自具有项 A、B 和 AB 的方差分析),n1= 因子 A 的每个水平下的观测值数。
具有两个以上水平的因子
- UDLA =
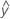 ...+ hα* Sqrt[MSE * (a - 1) / (a * n1)]
...+ hα* Sqrt[MSE * (a - 1) / (a * n1)] - LDLA =
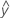 ...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
其中,MSE = 均方误(来自具有项 A、B 和 AB 的方差分析),a = 因子 A 中的因子水平数,n1 = 每个因子水平的观测值数。临界值 h= 取决于 alpha、正在绘制的均值数和 MSE 的自由度。您可以在纳尔逊1附录 B 中的表 B.1 中找到 h = 的值。
对于 .0.001 和 .0.1 范围以外的 alpha 值,决策限为:
- UDLA =
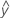 ...+ hα* Sqrt[MSE * (a - 1) / (a * n1)]
...+ hα* Sqrt[MSE * (a - 1) / (a * n1)] - LDLA =
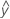 ...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
where MSE = mean square error (from an ANOVA with terms A, B, and AB), n1= number of observations at each level of the factor. and hα = absolute value (t(α2, df); where a2 = (1- (1- a )** (1 / a)) / 2 and df = nT - ab where nT = total number of observations in the sample,.
- L.S.Nelson (1983)。“Exact Critical Values for Use with the Analysis of Means”(用于均值分析的精确临界值),Journal of Quality Technology(质量技术期刊),第 15 期,第 40-44 页。
交互效应的决策上限和下限
决策限表明交互作用是否显著。决策上限 (UDL) 或决策下限 (LDL) 之外的点表明交互作用项统计意义显著。
以下列出的是针对因子 A 和 B 的交互作用决策上限和下限的一般公式。根据每个因子中的水平数和观测值数,项的定义将有所不同。
- UDLAB = hα* Sqrt[MSE * (q / (a * b * n)]
- LDLAB = –hα* Sqrt[MSE * (q / (a * b * n)]
其中 ha = 绝对值 (t(α2, dfe)),a = 因子 A 中的水平数,b = 因子 B 中的水平数,n = 因子之间每个交互作用项的观测值数,q = 交互效应 (a - 1)(b - 1) 的自由度,以及 dfe = 误差 abn - ab 的自由度。
因子 A 和 B 都具有两个水平
- α2 = a / 2
因子 A 具有两个水平,因子 B 具有两个以上水平
- α2 = (1- (1- a )** (1 / b)) / 2
其中 a = 因子 A 中的水平数,且 b = 因子 B 中的水平数。
因子 A 具有两个以上水平,因子 B 具有两个水平
- α2 = (1- (1- a )** (1 / a)) / 2
其中 a = 因子 A 中的水平数,且 b = 因子 B 中的水平数。
因子 A 和 B 具有两个以上水平
- α2 = (1- (1- a )** (1 /a * b)) / 2
其中 a = 因子 A 中的水平数,且 b = 因子 B 中的水平数。
