服从正态分布的数据的均值分析图
使用正态分布数据的均值分析图来确定数据中的主效应和交互效应是否统计意义显著。根据设计中的因子数,图表会显示一个主效应图或两个主效应图以及一个交互效应图。
- 交互效应图
-
使用交互效应图来检验因子之间没有交互作用的原假设。当数据包含两个因子时,Minitab 只显示一个交互效应图。
交互效应图显示了每个因子水平组合的平均度量。Minitab 绘制的中心线在零的位置,这表示不存在交互效应。决策限值基于您的数据和指定的显著性水平计算。使用双因子均值分析,首先评估交互作用效应。如果交互作用效应在统计意义上显著,那么,不考虑交互作用效应就无法解释主效应。
使用决策限值来检验交互效应的假设,如下所示:- 如果一个或多个效应超出决策限值,您可以得出两个因子之间的交互效应统计意义显著的结论。确定超出决策限值的点可能会有助于您解释交互作用。
- 如果效应未超出决策限值,则无法否定原假设。没有充分证据得出存在交互效应的结论。
- 主效应图
-
使用主效应图来检验“每个因子水平的总体均值等于指定显著性水平的整个总体均值”的原假设。Minitab 显示每个因子的一个主效应图。
主效应图显示每个因子水平的平均度量。中心线是所有样本的整体平均值。决策限值基于您的数据和指定的显著性水平计算。使用决策限值可检验主效应的假设,如下所示:- 如果样本均值超出决策限值,则可以否定原假设并得出组均值和整体均值之间的差值统计意义显著的结论。
- 如果样本均值未超出决策限值,则不能否定原假设。没有充分证据可以得出组均值和整体均值不同的结论。
如果所有因子水平均具有相同的观测值数,那么决策限将为直线。如果并非所有水平都具有相同的观测值数,决策限随着水平的变化而变化。
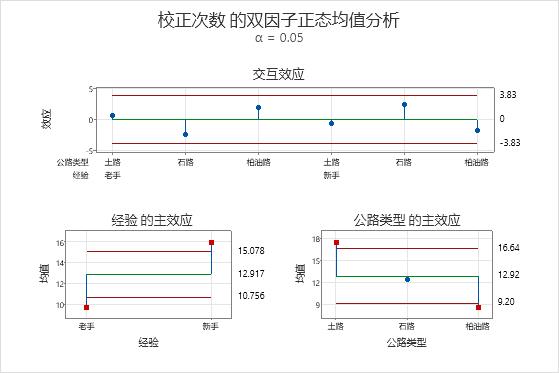
主要结果:主效应图、交互效应图
在该图中,交互作用效应正好在决策限内,这表示交互作用效应在统计意义上不显著。接着,评估主效应。下面的两个图显示两个因子的水平均值。主效应是均值和中心线之间的差值。
在经验的主效应图中,表示这两个高级和新手经验的因子水平均值的点不在决策限内。此条件表示其中的每个均值和总体均值之差在统计意义上显著。您可以得出高级司机的平均校正时间显著较低,新手司机的平均校正时间显著较高。
同样,在道路类型的主效应图中,土路和公路的主效应超出了决策限,这表明这些主效应在统计意义上显著。但是,砂石路的主效应在统计意义上不显著。
二项数据的均值图表分析
使用二项数据的均值图表分析可以识别异常大或异常小的比率。
- 如果样本比率超出决策限值,您可以否定原假设并得出组比率和整体比率之间的差值统计意义显著的结论。
- 如果样本比率未超出决策限值,则不能否定原假设。没有充分证据可以得出组比率和整体比率不同的结论。
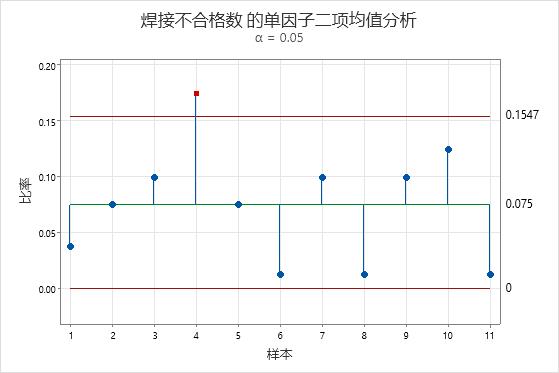
主要结果:单因子二项 ANOM 图
在此图中,样本 4 中的缺陷焊接比率超出了决策限值。此组中的缺陷焊接比率与总体比率之间的差值统计意义显著。
Poisson 数据的均值分析图表
使用 Poisson 数据均值分析图表来确定异常的较大或较小发生率。
- 如果发生率高于或低于决策限值,您可以否定原假设并得出组发生率和整体发生率之间的差分在统计意义上显著的结论。
- 如果样本均值未超出决策限值,则不能否定原假设。没有充分证据可以得出组发生率和整体发生率不同的结论。
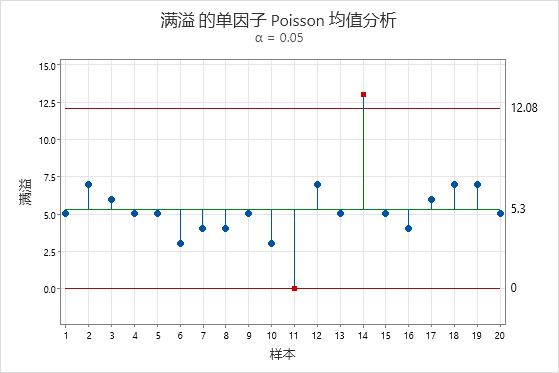
主要结果:单因子 Poisson ANOM 图
在该图中,第 11 台机器的溢出计数为 0,它异常小。第 14 台机器的溢出计数为 13,它异常大。经理为第 14 台机器安排了诊断工作以排除任何机械问题。
