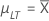
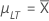
用于估计长期和短期标准差的无偏常量
- 用于估计长期标准差的无偏常量
-
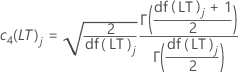
- 用于估计短期标准差的无偏常量
-
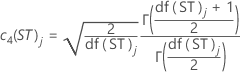
其中:
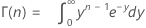
表示法
| 项 | 说明 |
|---|---|
| c4(LT)j | 计算第 j 个累积子组的长期无偏常量 |
| c4(ST)j | 计算第 j 个累积子组的短期无偏常量 |
| df(LT)j | 第 j 个子组的长期自由度 |
| df(ST)j | 第 j 个子组的短期自由度 |
短期标准差
- 包含无偏常量的短期标准差(默认设置)
-

- 不包含无偏常量的短期标准差
-
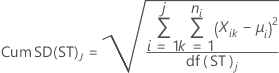
其中:
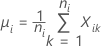
表示法
| 项 | 说明 |
|---|---|
| Cum SD(ST)j | 直至第 j 个子组的累积短期标准差 |
| c4(ST)j | 计算第 j 个累积子组的短期无偏常量 |
| df(ST)j | 第 j 个子组的短期自由度 |
长期标准差
- 不包含无偏常量的长期标准差(默认设置)
-
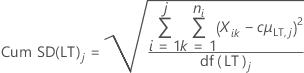
- 包含无偏常量的长期标准差
-
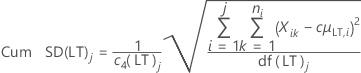
其中:
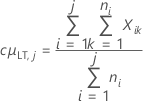
表示法
| 项 | 说明 |
|---|---|
| Cum SD(LT)j | 直至第 j 个子组的累积长期标准差 |
| c4(LT)j | 计算第 j 个累积子组的长期无偏常量 |
| df(LT)j | 第 j 个子组的长期自由度 |
长期过程均值
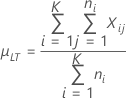
表示法
| 项 | 说明 |
|---|---|
| µLT |
长期均值或过程均值 μLT = cμLT,K 注意
|
长期过程标准差
σLT = Cum SD(LT)K
短期过程均值
- 如果已给定目标
- μST = T
- 如果给定了规格上限和下限(未给定目标)

- 如果给定了一个规格限(未给定目标)
- μST = μLT
表示法
| 项 | 说明 |
|---|---|
| µST | 短期均值 |
| T | 目标值 |
| µLT |
长期均值或过程均值 注意
|
短期过程标准差
σST = Cum SD(ST)K
有关更多信息,请转到Minitab 如何选择过程报告的短期统计量的居中值。
能力统计量
- CCpk
-

- Cp
-

- Cpk
-
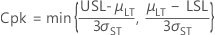
- CPL
-

- CPU
-

注意
Cp、Cpk 和 CCpk 表示潜在的过程能力。因此,这些公式使用短期变异性。
- Pp
-

- Ppk
-
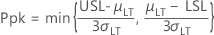
- PPL
-
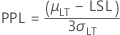
- PPU
-

注意
Pp 和 Ppk 表示实际的过程性能。因此,这些公式使用长期变异性。
自由度
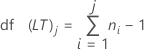
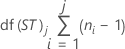
表示法
| 项 | 说明 |
|---|---|
| df(LT)j | 第 j 个子组的长期自由度 |
| df(ST)j | 第 j 个子组的短期自由度 |
概率
- P.LSL(LT)j
-
小于或等于第 j 个子组的规格下限的长期概率
P.LSL(LT) j = 1 – Φ(Z.LSL(LT)j)
- P.LSL(ST) j
-
小于或等于第 j 个子组的规格下限的短期概率
P.LSL(ST) j = 1 – Φ(Z.LSL(ST)j)
- P.USL(LT) j
-
大于或等于第 j 个子组的规格上限的长期概率
P.USL(LT) j = 1 – Φ(Z.USL(LT)j)
- P.USL(ST) j
-
大于或等于第 j 个子组的规格上限的短期概率
P.USL(ST) j = 1 – Φ(Z.LSL(ST)j)
- P.Total(LT) j
-
第 j 个子组超出规格的总(长期)概率
P.Total(LT) j = P.USL(LT)j + P.LSL(LT)j
- P.Total(ST)j
-
第 j 个子组超出规格的总(短期)概率
P.Total(ST)j = P.USL(ST)j + P.LSL(ST)j
基准 Z 值统计量
- Z.Bench(LT)j
-
第 j 个子组的基准 Z 值(长期)
Z.Bench(LT)j = Φ−1(P.Total(LT)j)
- Z.Bench(ST)j
-
第 j 个子组的基准 Z 值(短期)
Z.Bench(ST)j = Φ−1(P.Total(ST)j)
- Z.LSL(LT)j
-
第 j 个子组的规格下限 Z 值(长期)
Z.LSL(LT)j = (μLT – LSL) / Cum SD(LT)j
- Z.LSL(ST)j
-
第 j 个子组的规格下限 Z 值(短期)
Z.LSL(ST)j = (μST – LSL) / Cum SD(ST)j
- Z.USL(LT)j
-
第 j 个子组的规格上限 Z 值(长期)
Z.USL(LT)j = (USL – μLT) / Cum SD(LT)j
- Z.USL(ST)j
-
第 j 个子组的规格上限 Z 值(短期)
Z.USL(ST)j = (USL – μST) / Cum SD(ST)j
- Z.Shiftj
-
第 j 个子组的移位因子
Z.Shiftj = Z.Bench(ST)j – Z.Bench(LT)j