某质量工程师想要评估公司制造的灯泡的寿命。该工程师收集了一个含 100 个灯泡的随机样本,并记录灯泡在失效之前的照明时间。该工程师想要计算公差下限(在所有灯泡中,至少有 95% 的灯泡的照明时间超过此下限)。
- 打开样本数据 灯泡点亮时间.MWX.
- 选择。
- 从下拉列表中,选择一个或多个样本,每列一个并输入小时数。
- 单击选项。
- 从公差区间中,选择下限。
- 单击每个对话框中的确定。
解释结果
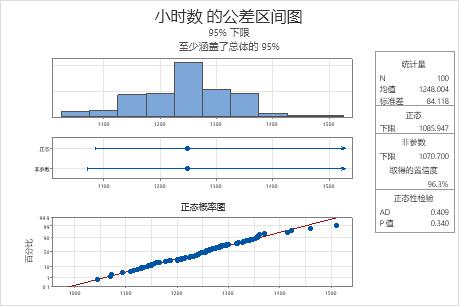
正态概率图显示标绘点形成近似直线,这表明数据服从正态分布。而且,正态性检验的 p 值为 0.340,大于显著性水平 (α = 0.05)。因此,证据不足,无法判定数据不服从正态分布。工程师可以使用正态方法的结果。
正态下限为 1085.947,因此工程师有 95% 的信心确信,在所有灯泡中,至少有 95% 的灯泡的照明时间大约超过 1086 个小时。对于所有灯泡,平均照明时间大约为 1248 个小时,标准差大约为 84.1。
方法
| 置信水平 | 95% |
|---|---|
| 区间中总体的百分比 | 95% |
统计量
| 变量 | N | 均值 | 标准差 |
|---|---|---|---|
| 小时数 | 100 | 1248.004 | 84.118 |
95% 公差下限
| 变量 | 正态方法 | 非参数方法 | 取得的置信度 |
|---|---|---|---|
| 小时数 | 1085.947 | 1070.700 | 96.3% |