请选择您所选的方法或公式。
极大似然估计
通过相对于参数最大化似然函数来计算分布中参数的极大似然估计值。对于给定的数据集,极大似然估计值是最可能的分布参数值。
Newton-Raphson 算法用于计算分布参数的极大似然估计值。Newton-Raphson 算法是用于计算函数最大值的迭代数值方法。1
注意
对于除对数正态分布外的所有分布,Minitab 使用极大似然方法来计算参数估计值。对于对数正态分布,Minitab 将计算无偏参数估计值。
概率分布
对数正态分布
 |
|
| CDF |
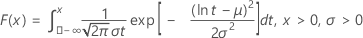 |
| 均值 |
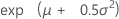 |
| 标准差 |
 |
| 项 | 说明 |
|---|---|
| μ | 尺度参数 |
| σ | 形状参数 |
Gamma 分布
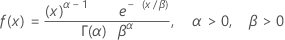 |
|
| CDF |
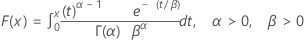 |
| 均值 | αβ |
| 标准差 | αβ2 |
| 项 | 说明 |
|---|---|
| α | 形状参数 |
| β | 尺度参数 |
指数分布
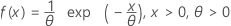 |
|
| CDF |
 |
| 均值 | θ |
| 标准差 | θ |
| 项 | 说明 |
|---|---|
| θ | 尺度参数 |
最小极值分布
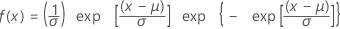 |
|
| CDF |
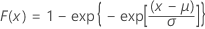 |
| 均值 |
 |
| 标准差 |
 |
| 项 | 说明 |
|---|---|
| μ | 位置参数 |
| σ | 尺度参数 |
| γ | Euler 常量(大约等于 0.5772) |
Weibull 分布
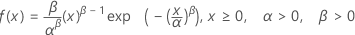 |
|
| CDF |
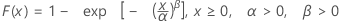 |
| 均值 |
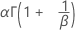 |
| 标准差 |
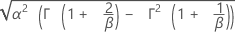 |
| 项 | 说明 |
|---|---|
| α | 尺度参数 |
| β | 形状参数 |
最大极值分布
 |
|
| CDF |
 |
| 均值 |
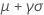 |
| 标准差 |
 |
| 项 | 说明 |
|---|---|
| μ | 位置参数 |
| σ | 尺度参数 |
| γ | Euler 常量(大约等于 0.5772) |
Logistic 分布
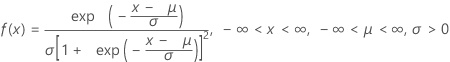 |
|
| CDF |
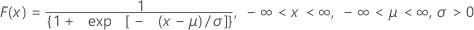 |
| 均值 | μ |
| 标准差 |
 |
| 项 | 说明 |
|---|---|
| μ | 位置参数 |
| σ | 尺度参数 |
对数 Logistic 分布
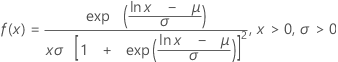 |
|
| CDF |
 |
| 均值 |
 |
| 标准差 |
 |
| 项 | 说明 |
|---|---|
| μ | 位置参数 |
| σ | 尺度参数 |
1 W. Murray, Ed. (1972)。Numerical Methods for Unconstrained Optimization(非约束优化的数值方法)。Academic Press。
