公差区间（非正态分布）的主要结果

请完成以下步骤来解释公差区间。

关于本主题

步骤 1：评估数据的分布拟合
步骤 2：检查相应方法的公差区间

步骤 1：评估数据的分布拟合

Minitab 为使用分布的方法和非参数方法提供公差区间。如果您能够肯定地假设数据服从分布，则采用的公差区间可以是使用该分布的方法的区间如果您不能肯定地假设数据服从分布，则必须尝试其他分布或者使用非参数方法的公差区间。

要确定能否假设数据服从分布，请比较 Anderson-Darling 检验的 p 值与显著性水平 (α)。显著性水平 0.05 表示当数据实际上服从分布时，判定数据不服从分布的风险为 5%。

P 值 ≤ α：数据不服从分布（否定 H₀）: 如果 p 值小于或等于显著性水平，则可以得出数据不服从分布的结论。在这种情况下，您必须尝试其他分布或者使用非参数方法的公差区间。
P 值 > α：证据不足，无法得出数据不服从分布的结论（无法否定 H₀）: 如果 p 值大于显著性水平，则证据不足，无法得出数据不服从分布的结论。在这种情况下，采用的公差区间可以是使用该分布的方法的区间。

主要结果：概率图和 p 值

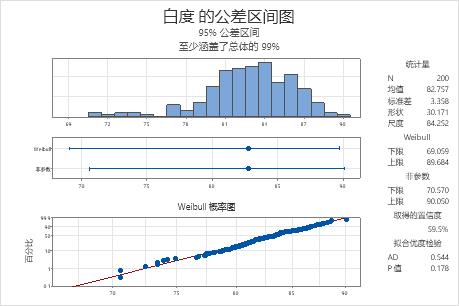
概率图显示，绘制的点沿着 Weibull 分布拟合线落位。而且，拟合优度检验的 p 值为 0.178，这大于显著性水平 0.05。由于无法认定数据不遵循 Weibull 分布，因此可以对 Weibull 分布使用此区间。

步骤 2：检查相应方法的公差区间

Minitab 为使用分布的方法和不假定特定分布的非参数方法提供公差区间。您可以创建双侧公差区间，也可以创建提供上限或下限的单侧公差区间。

双侧

使用双侧区间可以确定包含特定最小百分比的总体测量值的区间。

统计量

变量	N	均值	标准差
白度	200	82.757	3.358

95% 公差区间

变量	Weibull 方法	非参数方法	取得的置信度
白度	(69.059, 89.684)	(70.570, 90.050)	59.54%

主要结果：95% 公差区间

Weibull 区间的范围大约为从 69.1 到 89.7，因此制造商对至少 99% 所有批次的纸浆将落位于此区间可以具有 95% 的置信水平。对于所有批次的纸浆，平均亮度水平为大约 82.8。

上限

使用上限可以确定超出特定最小百分比的总体测量值的限值。

95% 公差上限

变量	Weibull 方法	非参数方法	取得的置信度
白度	89.131	90.050	86.60%

主要结果：95% 公差上限

在此示例中，由于 Weibull 上限为 89.131，因此所有批次纸浆中 99% 的纸浆具有 89.131 或更低白度的置信度为 95%。如果您不能假定数据服从 Weibull 分布，请找出可拟合的其他分布或者考虑非参数上限 90.50。对于非参数方法，取得的置信度为 86.60%，它远小于目标值 95%。此结果表示，您的样本数量太少，导致非参数方法不准确。

下限

使用下限可以确定小于特定最小百分比的总体测量值的限值。

95% 公差下限

变量	Weibull 方法	非参数方法	取得的置信度
白度	71.105	70.570	86.60%

主要结果：95% 公差下限

在此示例中，由于 Weibull 下限为 71.105，因此所有批次纸浆中 99% 的纸浆具有 71.105 或更高白度的置信度为 95%。如果您不能假定数据服从 Weibull 分布，请找出可拟合的其他分布或者考虑非参数下限 70.570。对于非参数方法，取得的置信度为 86.60%，它远小于目标值 95%。此结果表示对此结果表示，您的样本数量太少，导致非参数方法不准确。