公差区间（非正态分布）的公差区间

请查找相关定义和解释指导，了解非正态分布的公差区间中的公差区间。

关于本主题

参数分布方法
非参数方法
取得的置信度
公差区间图

参数分布方法

公差区间是产品的特定质量特征值的范围，该区间可能涵盖指定最低百分比的当前或未来产品产量。如果能够可靠地假设样本来自服从该分布的总体，则使用参数分布的方法。

如果您的数据服从参数分布，则使用该分布的方法比非参数方法更准确和经济。只要所选分布适合您的数据，使用分布的方法就可以通过较少的观测值取得较小的边际误差。

使用参数分布的方法对于严重偏离该分布的情况并不是稳健的方法。如果您对于总体分布并不确定，则使用个体分布标识概述。如果您知道总体分布不在非正态公差区间的分布列表中，则使用非参数方法。

解释

双侧

使用双侧区间可以确定包含特定最小百分比的总体测量值的区间。

在此示例中，通过使用 Weibull 方法，您能够以 95% 的置信度确信，所有白度测量值中至少 99% 的测量值大约介于 69.1 至 89.7 之间。

95% 公差区间

变量	Weibull 方法	非参数方法	取得的置信度
白度	(69.059, 89.684)	(70.570, 90.050)	59.54%

上限

使用上限可以确定超出特定最小百分比的总体测量值的限值。

在此示例中，通过使用 Weibull 方法，您能够以 95% 的置信度确信，所有白度测量值中至少 99% 的测量值小于 89.131。此限值用于与双侧示例相同的数据。对于 Weibull 方法，单侧上限小于双侧区间的上限。

95% 公差上限

变量	Weibull 方法	非参数方法	取得的置信度
白度	89.131	90.050	86.60%

下限

使用下限可以确定小于特定最小百分比的总体测量值的限值。

在此示例中，通过使用 Weibull 方法，您能够以 95% 的置信度确信，所有白度测量值中至少 99% 的测量值大于 71.105。此限值用于与双侧示例相同的数据。对于 Weibull 方法，单侧下限大于双侧区间的下限。

95% 公差下限

变量	Weibull 方法	非参数方法	取得的置信度
白度	71.105	70.570	86.60%

非参数方法

公差区间是产品的特定质量特征值的范围，该区间可能涵盖指定最低百分比的当前或未来产品产量。如果您不能可靠地假设样本来自 Minitab 中的参数分布，则必须使用非参数方法公差区间。

非参数方法仅要求数据为连续数据。但是，非参数方法要求样本达到很大数量，才能保证结果准确性。如果样本数量不够多，则此非参数区间为无信息区间，其范围为从负无穷大到正无穷大。在这种情况下，Minitab 将根据数据范围显示一个有限区间。结果，所取得的置信水平将远远低于目标置信水平。

解释

双侧

使用双侧区间可以确定包含特定最小百分比的总体测量值的区间。

在此示例中，通过使用非参数方法，您能够以 59.54% 的置信度确信，所有白度测量值中至少 99% 的测量值介于 70.570 至 90.050 之间。取得的置信度小于目标值 95%。这表示您的样本数量太少，导致非参数方法不起作用。

95% 公差区间

变量	Weibull 方法	非参数方法	取得的置信度
白度	(69.059, 89.684)	(70.570, 90.050)	59.54%

上限

使用上限可以确定超出特定最小百分比的总体测量值的限值。

在此示例中，通过使用非参数方法，您能够以 86.6% 的置信度确信，所有白度测量值中至少 99% 的测量值小于 90.050。此限值用于与双侧示例相同的数据。取得的置信度远小于目标值 95%。此结果表示，您的样本数量太少，导致非参数方法不准确。

95% 公差上限

变量	Weibull 方法	非参数方法	取得的置信度
白度	89.131	90.050	86.60%

下限

使用下限可以确定小于特定最小百分比的总体测量值的限值。

在此示例中，通过使用非参数方法，您能够以 86.6% 的置信度确信，所有白度测量值中至少 99% 的测量值大于 70.570。此限值用于与双侧示例相同的数据。取得的置信度远小于目标值 95%。此结果表示，您的样本数量太少，导致非参数方法不准确。

95% 公差下限

变量	Weibull 方法	非参数方法	取得的置信度
白度	71.105	70.570	86.60%

取得的置信度

对于非参数方法，Minitab 将计算所达到的置信水平。这是从样本中获取的精确置信水平。它通常不会小于目标置信水平，除非您的样本数量太小。

如果样本数量不够多，则非参数区间将是从负无限到正无限的非信息性区间。在这种情况下，Minitab 将根据数据范围显示一个有限区间。因此，取得的置信水平远低于目标置信水平。

解释

双侧

使用双侧区间可以确定包含特定最小百分比的总体测量值的区间。

在此示例中，通过使用非参数方法，您能够以 59.54% 的置信度确信，所有白度测量值中至少 99% 的测量值介于 70.57 至 90.050 之间。取得的置信度小于目标值 95%。这表示您的样本数量太少，导致非参数方法不起作用。

95% 公差区间

变量	Weibull 方法	非参数方法	取得的置信度
白度	(69.059, 89.684)	(70.570, 90.050)	59.54%

上限

使用上限可以确定超出特定最小百分比的总体测量值的限值。

在此示例中，取得的置信度为 86.60%。取得的置信度远小于目标值 95%。此结果表示，您的样本数量太少，导致非参数方法不准确。

95% 公差上限

变量	Weibull 方法	非参数方法	取得的置信度
白度	89.131	90.050	86.60%

下限

使用下限可以确定小于特定最小百分比的总体测量值的限值。

在此示例中，取得的置信度为 86.60%。取得的置信度远小于目标值 95%。此结果表示，您的样本数量太少，导致非参数方法不准确。

95% 公差下限

变量	Weibull 方法	非参数方法	取得的置信度
白度	71.105	70.570	86.60%

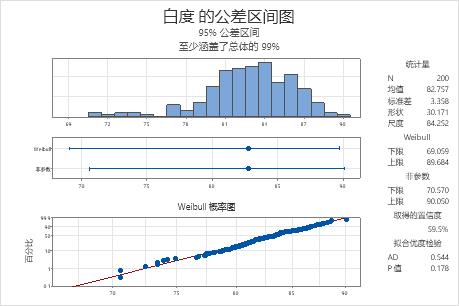
公差区间图

公差区间图包含以下图形和统计量：

直方图：显示样本数据的分布。直方图上的每个条形表示区间内数据的频率。
区间图：显示每种方法的公差区间的均值、上限和/或下限。区间末端的垂直线代表区间界限，而箭头表示相应的区间侧没有界限。
概率图：显示数据对分布的拟合优度。如果数据服从分布，则概率图上的数据点沿假定的分布拟合线分布。
统计量表：显示样本数量、均值和标准差。
参数分布表：显示使用参数分布的方法的上限和/或下限。
非参数表：显示非参数方法公差区间的上限和/或下限，以及所达到的置信水平。
拟合优度检验表：显示 p 值和 Anderson-Darling 检验值。要确定能否假设数据服从分布，请比较检验的 p 值与显著性水平 (α)。如果 p 值小于或等于显著性水平，则可以得出数据不服从分布的结论。在这种情况下，请尝试备择分布，或者如果取得的置信水平接近目标水平，则使用非参数方法的公差区间。

解释

概率图显示，绘制的点沿着 Weibull 分布拟合线落位。而且，拟合优度检验的 p 值为 0.178，这大于显著性水平 0.05。由于无法认定数据不遵循 Weibull 分布，因此可以对 Weibull 分布使用此区间。

Weibull 区间的范围大约为从 69.1 到 89.7，因此制造商对至少 99% 所有批次的纸浆将落位于此区间可以具有 95% 的置信水平。对于所有批次的纸浆，平均亮度水平为大约 82.8。