对数正态分布
如果随机变量的对数是正态分布的,请使用对数正态分布。当随机变量大于 0 时使用。例如,对数正态分布可用于可靠性分析和金融应用,例如为股价行为建模。
对数正态分布是由其位置和尺度参数定义的连续分布。3 参数对数正态分布由其位置、尺度和阈值参数定义。
Gamma 分布
使用 Gamma 分布可以对向右偏斜且大于 0 的正数据值进行建模。Gamma 分布通常用在可靠性生存研究中。例如,Gamma 分布可以描述电气组件失效的时间。大多数特殊类型的电气组件几乎会同时失效,但是少数组件将在很长时间后才会失效。
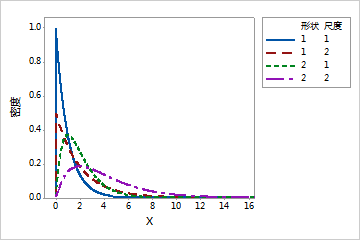
当形状参数为整数时,Gamma 分布有时称为 Erlang 分布。Erlang 分布通常用于排队理论应用中。
指数分布
可使用指数分布对连续 Poisson 过程中的两个事件之间的时间进行建模。假设独立事件以恒定速率发生。
此分布应用广泛(包括产品和系统的可靠性分析、排队理论以及马尔可夫链)。
- 电气组件的失效时间
- 客户到达终端的间隔时间
- 客户排队等待的服务时间
- 拖欠付款的时间(信用风险建模)
- 放射性核衰变的时间
对于单参数指数分布,阈值为零,且分布由其尺度参数定义。对于单参数指数分布,尺度参数等于均值。
无记忆的含义是什么?
指数分布的重要属性为它是无记忆的。事件的发生机会不依赖于过去的试验。因此,发生率保持不变。
该无记忆属性指示组件的剩余寿命与其当前使用年限无关。例如,抛硬币的随机试验体现了无记忆属性。经过磨损并在使用年限后期更容易失效的系统便不是无记忆的。
最小和最大极值分布
最小极值分布
最大极值分布
Weibull 分布
Weibull 分布是一个多功能分布,可用来对工程制造、医学研究、质量控制、财务和气候领域中的广泛应用进行建模。例如,此分布常与可靠性分析一起用于对失效时间数据进行建模。Weibull 分布也用于对能力分析中的偏斜过程数据进行建模。
Weibull 分布由其形状、尺度和阈值参数描述,也称为 3 参数 Weibull 分布。阈值参数为零的情况称为双参数 Weibull 分布。只能为正变量定义双参数 Weibull 分布。3 参数 Weibull 分布可使用零和负数据,但双参数 Weibull 分布只能使用大于零的数据。
根据其参数的值,Weibull 分布可以具有各种形状。
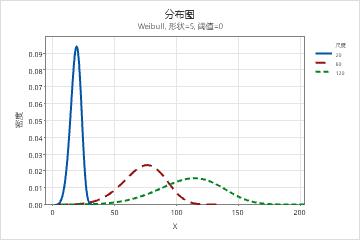
- 形状参数的效应
- 形状参数描述数据的分布方式。形状 3 接近于正态曲线。较低的形状值(如 1)将给出右偏斜曲线。较高的形状值(如 10)将给出左偏斜曲线。
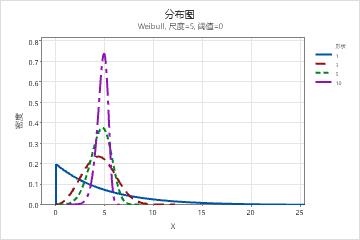
- 尺度参数的效应
- 尺度或特征寿命是数据的 63.2 百分位数。尺度定义 Weibull 曲线相对于阈值的位置,这与均值定义正态曲线位置的方式相类似。例如,尺度为 20 表示 63.2% 的设备将在阈值时间过后的前 20 小时内失效。
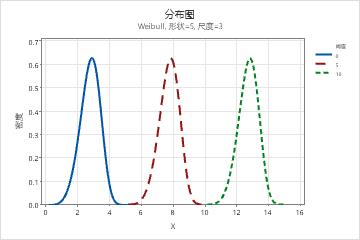
- 阈值参数的效应
- 阈值参数描述分布离 0 位置的偏移。负阈值使分布向左偏移,正阈值使分布向右偏移。所有数据必须大于阈值。双参数 Weibull 分布与阈值为 0 的 3 参数 Weibull 分布相同。例如,3 参数 Weibull (3,100,50) 与双参数 Weibull (3,100) 的形状和散布相同,但会向右偏移 50 个单位。
Logistic 分布
使用 Logistic 分布可对与正态分布相比尾部更长且峰度更高的数据分布进行建模。
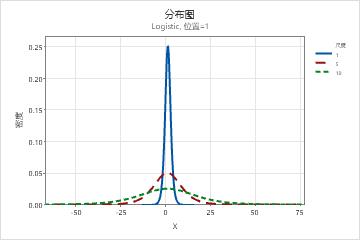
- 尺度参数的效应
- 下图显示了 Logistic 分布上不同尺度参数值的效应。
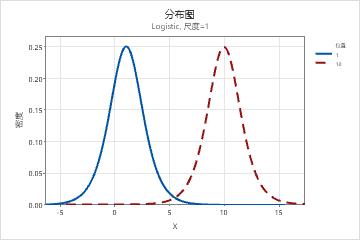
- 位置参数的效应
- 下图显示了 Logistic 分布上不同位置参数值的效应。
对数 Logistic 分布
当变量的对数呈对数 Logistic 分布时,可使用对数 Logistic 分布。例如,对数 Logistic 分布可用于生长模型中,以及用于对生物统计和经济等领域中的二元响应进行建模。
对数 Logistic 分布是由其尺度和位置参数定义的连续分布。3 参数对数 Logistic 分布由其尺度、位置和阈值参数定义。
对数 Logistic 分布也称为 Fisk 分布。
