关于本主题
游程图
游程图按照过程数据的收集顺序绘制过程数据。 使用游程图可以在数据中查找可指示是否存在特殊原因变异的模式或趋势。
解释
数据中的模式指示变异是由于应当调查和更正的特殊原因引起的。但是,常规原因变异是固有的或作为过程中正常部分的变异。当只有常规原因(而非特殊原因)影响过程输出时,过程是稳定的。如果过程中只存在常规原因变异,则数据将表现出随机行为。
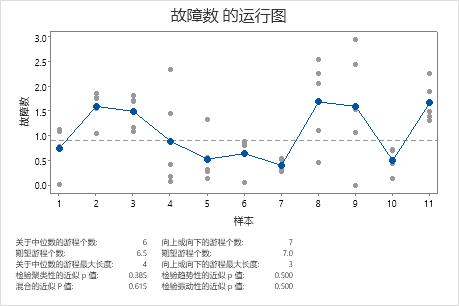
中位数附近的游程数
围绕中位数的游程数是中位数上下发生的总游程数。
中位数附近的游程是位于中心线同一侧的一个或多个连续的点。当连接这些点的线与中心线相交时,游程结束。新的游程从下一个标绘点开始。
解释
- 游程 1 包括点 1。
- 游程 2 包括点 2 和 3。
- 游程 3 包括点 4、5、6 和 7。
- 游程 4 包括点 8 和 9。
- 游程 5 包括点 10。
- 游程 6 包括点 11。

中位数附近的预期游程数
中位数附近预期的游程数是数据随机分布时您预期数据中包含的游程数。
解释
将预期的游程数与实际的游程数进行比较。如果实际的游程数大于预期的游程数,则表明数据来自两个总体(混合)。如果实际的游程数小于预期的游程数,则表明存在数据聚类。使用 p 值可以检验统计显著性。

中位数附近的游程最大长度
最长游程中位于中位数上方或下方的点数。位于中心线上的点属于中位数下方的游程。
解释

聚类的近似 p 值
P 值是一个概率,用来度量否定原假设的证据。概率越低,否定原假设的证据越充分。
使用 p 值可以确定数据是否随机分布。原假设是数据随机分布。
解释
如果 p 值小于指定的显著性水平,则表明存在聚类趋势。通常,显著性水平(用 α 或 alpha 表示)为 0.05 即可。显著性水平 0.05 指示当数据实际上随机分布时,判定存在非随机模式的风险为 5%。
- P 值 ≤ α:平均差值显著不同(否定 H0)
- 如果 p 值小于或等于显著性水平,则否定原假设。您可以得出数据不是随机分布的结论。
- P 值 > α:均值的差值不是显著不同(无法否定 H0)
- 如果 p 值大于显著性水平,则无法否定原假设。您的证据不足,无法得出数据具有非随机模式的结论。但是,您也无法得出数据随机分布的结论。

混合的近似 p 值
P 值是一个概率,用来度量否定原假设的证据。概率越低,否定原假设的证据越充分。
使用 p 值可以确定数据是否随机分布。原假设是数据随机分布。
解释
如果 p 值小于指定的显著性水平,则表明存在混合趋势。通常,显著性水平(用 α 或 alpha 表示)为 0.05 即可。显著性水平 0.05 指示当数据实际上随机分布时,判定存在非随机模式的风险为 5%。
- P 值 ≤ α:平均差值显著不同(否定 H0)
- 如果 p 值小于或等于显著性水平,则否定原假设。您可以得出数据不是随机分布的结论。
- P 值 > α:均值的差值不是显著不同(无法否定 H0)
- 如果 p 值大于显著性水平,则无法否定原假设。您的证据不足,无法得出数据具有非随机模式的结论。但是,您也无法得出数据随机分布的结论。

向上或向下的游程数
向上或向下的游程数是数据中向上和向下的游程总数。
向上的游程是连续点仅上升的向上游程。向下的游程是连续点仅下降的向下游程。当方向(向上或向下)改变时,游程结束。例如,当前一个值较小时,一个向上的游程将开始并继续,直到前一个值大于下一个点,这时向下的游程即告开始。
Minitab 将连续的相等观测值的平游程计入向下游程的一部分。
解释
- 点 2 标记游程 1 的结尾。
- 点 5 标记游程 2 的结尾。
- 点 6 标记游程 3 的结尾。
- 点 7 标记游程 4 的结尾。
- 点 8 标记游程 4 的结尾。
- 点 10 标记游程 6 的结尾。
- 点 11 标记游程 7 的结尾。

如何解释平游程
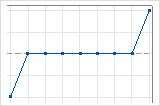
3 个向上和向下的游程
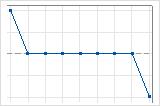
1 个向下的游程
向上或向下的预期游程数
预期的向上或向下游程数是数据随机分布时您预期数据中包含的游程数。
解释
将预期的游程数与实际的游程数进行比较。如果实际的游程数大于预期的游程数,则可能表明数据中存在振动。如果实际的游程数小于预期的游程数,则可能表明数据中存在趋势。使用 p 值可以检验显著性。

向上或向下的游程最大长度
向上或向下的最长游程中的点数。
解释

趋势的近似 p 值
P 值是一个概率,用来度量否定原假设的证据。概率越低,否定原假设的证据越充分。
使用 p 值可以确定数据是否随机分布。原假设是数据随机分布。
解释
如果 p 值小于指定的显著性水平,则表明存在趋势倾向。通常,显著性水平(用 α 或 alpha 表示)为 0.05 即可。显著性水平 0.05 指示当数据实际上随机分布时,判定存在非随机模式的风险为 5%。
- P 值 ≤ α:平均差值显著不同(否定 H0)
- 如果 p 值小于或等于显著性水平,则否定原假设。您可以得出数据不是随机分布的结论。
- P 值 > α:均值的差值不是显著不同(无法否定 H0)
- 如果 p 值大于显著性水平,则无法否定原假设。您的证据不足,无法得出数据具有非随机模式的结论。但是,您也无法得出数据随机分布的结论。

振动的近似 p 值
P 值是一个概率,用来度量否定原假设的证据。概率越低,否定原假设的证据越充分。
使用 p 值可以确定数据是否随机分布。原假设是数据随机分布。
解释
如果 p 值小于指定的显著性水平,则表明存在振动趋势。通常,显著性水平(用 α 或 alpha 表示)为 0.05 即可。显著性水平 0.05 指示当数据实际上随机分布时,判定存在非随机模式的风险为 5%。
- P 值 ≤ α:平均差值显著不同(否定 H0)
- 如果 p 值小于或等于显著性水平,则否定原假设。您可以得出数据不是随机分布的结论。
- P 值 > α:均值的差值不是显著不同(无法否定 H0)
- 如果 p 值大于显著性水平,则无法否定原假设。您的证据不足,无法得出数据具有非随机模式的结论。但是,您也无法得出数据随机分布的结论。

