原始数据和变换后数据的概率图
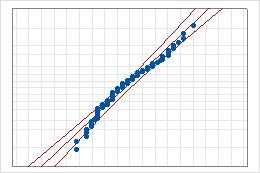
- 中线
- 基于极大似然参数估计的分布的预期百分位数。
- 置信限线
- 左侧曲线表示百分位数的置信区间下限。右侧曲线表示百分位数的置信区间上限。
解释
使用正态概率图可以评估原始数据和变换后数据对正态分布的服从程度。
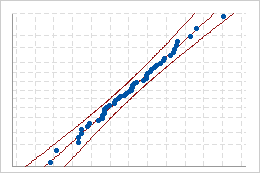
好拟合
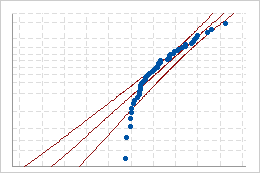
差拟合
注意
如果原始数据是正态分布数据,Minitab 将仅显示单个概率图,并且不执行 Johnson 变换。
N
样本中非缺失值的个数。N 是所有观测值的计数。
| 合计 | N | N* |
|---|---|---|
| 149 | 141 | 8 |
解释
使用 N 估计样本数量。
重要信息
在解释很小或很大样本的结果时请务必谨慎。如果您的样本很小,则拟合优度检验可能没有足够的功效来检测与分布存在显著偏差的情况。如果您的样本很大,则该检验的功效可能很高,从而可以检测到与分布的微小但不具实际意义的偏差。除 p 值以外,还要使用概率图评估分布拟合。
AD
Anderson-Darling 拟合优度统计量 (AD) 用来度量拟合线(基于所选分布)和非参数阶梯函数(基于数据点)之间的偏差。Anderson-Darling 统计量是指分布尾中加权更重的平方距离。
解释
Minitab 使用 Anderson-Darling 统计量计算 p 值。P 值是一个概率,用来度量否定原假设(即数据服从分布)的证据。
通常,如果 Anderson-Darling 统计量明显很小,则表明数据能够更紧密地服从分布。但是,当不同分布的 AD 值接近时,请避免直接比较这些值,因为不同分布的 AD 统计量的分布各不相同。为了更好地比较对不同分布的拟合,请使用额外的标准,如概率图、p 值和过程知识。
P 值
对于原始数据值和变换后的数据值,Minitab 报告 Anderson-Darling (AD) 正态性检验的 p 值。P 值是一个概率,用来度量否定原假设的证据。对于 AD 正态性检验,原假设是数据服从正态分布。因此,较小的 p 值会提供更强的证据来说明数据不服从正态分布。
解释
使用 p 值可以评估原始数据和变换后的数据是否服从正态分布。较大的 p 值通常表明能够更好地拟合数据。
- P 值小于 alpha 表明正态分布不是好拟合。
- P 值大于或等于 alpha 表明证据不足以说明分布拟合差。您可以假设数据服从正态分布。
如果 Johnson 变换有效,则变换后数据的 p 值大于 alpha。
重要信息
在解释很小或很大样本的结果时请务必谨慎。如果您的样本很小,则拟合优度检验可能没有足够的功效来检测与分布存在显著偏差的情况。如果您的样本很大,则该检验的功效可能很高,从而可以检测到与分布的微小但不具实际意义的偏差。除 p 值以外,还要使用概率图评估分布拟合。
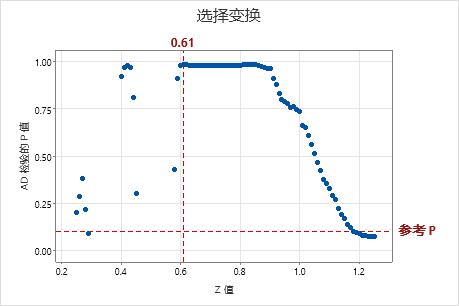
选择变换图
选择变换图绘制为不同 Johnson 变换函数的每个 Z 值计算的 AD 正态性检验 p 值。为找到最优的 Z,Johnson 变换将范围在 0.25 至 1.25 之间,递增量为 0.01 的 Z 网格用于范围广泛的分布。Minitab 计算每个 Z 的变换数据的 p 值,并选择具有最大 p 值的变换函数,该 p 值大于您指定用于分析的 p 值标准。
解释
使用选择变换图可以直观地表示如何选择能够以最佳方式拟合数据的 Johnson 变换函数。水平参考线显示指定用于分析的 p 值标准。垂直参考线显示可生成最佳拟合的变换的 Z 值。此最大 Z 值对应于 AD 正态性检验的最小 p 值。
注意
该图下方的表(此处未显示)显示最佳变换函数的参数估计值。有关 Minitab 用于 Johnson 变换函数的算法的更多信息,请转到个体分布标识中的变换方法和公式并单击“Johnson 变换的方法和公式”。
最佳拟合的 P 值
最佳拟合的 p 值指示 Johnson 变换的 p 值,该变换可将已变换数据最佳拟合为正态分布。此 p 值舍入到最近的千分位数,还显示在变换后数据的概率图上。
有关如何解释 p 值的信息,请参见有关 p 值的部分。
有关 Minitab 选择具有最佳拟合的 Johnson 变换函数的信息,请参见有关“选择变换”图的部分。
最佳拟合的 Z
最佳拟合的 Z 值指示 Johnson 变换函数的 Z 值,该变换可将已变换数据最佳拟合为正态分布。最优 Z 值对应于最佳拟合的 p 值,如最佳变换图上所示。
有关 Minitab 使用 Z 值选择具有最佳拟合的 Johnson 变换函数的信息,请参见有关选择变换图的部分。
最佳变换类型
Johnson 变换以最优方式选择以下三个分布系列中的一个系列:SB、SL 和 SU,其中 B、L 和 U 分别指有界变量、对数正态变量和无界变量。Minitab 使用选定的分布函数将数据变换为服从正态分布。
有关 Minitab 用来定义 Johnson 变换函数的算法的更多信息,请转到个体分布标识中的变换方法和公式并单击“Johnson 变换的方法和公式”。
Johnson 变换函数
Minitab 显示生成最佳拟合的 Johnson 变换函数的参数。Minitab 使用此函数变换原始数据。
例如,假设 Johnson 变换函数为 0.762475 + 0.870902 × Ln((X – 46.3174) / (59.6770 – X))。如果 X 的原始数据值为 50,则按如下方式计算变换后数据值 50:0.762475 + 0.870902 × Ln((50 – 46.3174) / (59.6770 – 50)),结果等于 –0.07893。
注意
要将变换后的所有值存储在工作表中,请在执行分析时输入存储列。
有关 Minitab 用来定义 Johnson 变换函数的算法的更多信息,请转到个体分布标识中的变换方法和公式并单击“Johnson 变换的方法和公式”。
