Box-Cox 变换
Box-Cox 变换估计 lambda 值(如下表所示),该值最小化标准式变换的变量的标准偏差。由此生成的变换是 Yλ(当 λ ҂ 0 时)及 ln Y(当 λ = 0时)。
Box-Cox 方法通过多种变换类型进行搜索。下表显示了一些常见的变换,其中 Y' 是数据 Y 的变换。
| Lambda (λ) 值 | 变换 |
|---|---|
 |
 |
 |
 |
 |
 |
 |
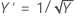 |
 |
 |
Johnson 变换的算法
Johnson 变换将选择三种分布系列中最优的一种系列来变换数据,使数据服从正态分布。
| Johnson 系列 | 变换函数 | 极差 |
|---|---|---|
| SB | γ + η ln [(x – ε) / (λ + ε – x)] | η,λ > 0,–∞ < γ < ∞,–∞ < ε < ∞,ε < x < ε + λ |
| SL | γ + η ln (x – ε) | η > 0,–∞ < γ < ∞,–∞ < ε < ∞,ε < x |
| SU | γ + η Sinh–1 [(x – ε) / λ],其中
Sinh–1(x) = ln [x + sqrt (1 + x2)] |
η,λ > 0,–∞ < γ < ∞,–∞ < ε < ∞,–∞ < x < ∞ |
该算法使用以下过程:
- 考虑了 Johnson 系统中几乎所有的潜在变换函数。
- 使用 Chou 等人描述的方法估计函数中的参数。1
- 使用变换函数变换数据。
- 计算变换数据的 Anderson-Darling 统计量和对应 p 值。
- 选择具有最大 p 值的变换函数,该 p 值大于您在变换对话框中指定的 p 值标准(默认值为 0.10)。否则,将没有适用的变换。
表示法
| 项 | 说明 |
|---|---|
| SB | 已限定变量的 Johnson 系列分布 (B) |
| SL | 使用对数正态变量的 Johnson 系列分布 (L) |
| SU | 未限定变量的 Johnson 系列分布 (U) |
有关 Johnson 变换的更多信息,请参见 Chou 等人的文献。1 Minitab 将使用 Anderson-Darling 检验替换该文本中使用的 Shapiro-Wilks 检验。
有关概率图、百分位数及其置信区间的信息,请转到个体分布标识中分布的方法和公式。
1 Y. Chou、A.M. Polansky 和 R.L. Mason (1998)。“Transforming Nonnormal Data to Normality in Statistical Process Control”(在统计过程控制中将非正态数据变换为正态数据),Journal of Quality Technology(质量技术杂志),第 30 期,4 月,第 133 到 141 页。
