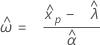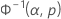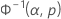概率图
概率图包括：
- 一些点，它们是顺序数据集的对应概率的估计百分位数。
- 中线，它们是基于极大似然参数估计值的分布的预期百分位数。如果分布提供对数据的良好拟合，这些点将沿中线分布。
估计的概率
Minitab 使用下列方法估计用来计算标绘点的概率 (P)。
- 中位数等级（Benard 方法）
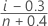
- 均值等级（Herd-Johnson 估计值）
- 修正后 Kaplan-Meier (Hazen)
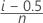
- Kaplan-Meier 乘积限估计值
表示法
| 项 | 说明 |
|---|---|
| n | 观测值个数 |
| ii | 第 i 个顺序观测值 x(i) 的等级，其中 x(1)、x(2)、...x(n) 是顺序统计量，或者按照从最小到最大排序的数据。 |
标绘点
概率图中间线是使用该表中的 x 和 y 坐标计算值构造的。
| 分布 | x 坐标 | y 坐标 |
|---|---|---|
| 最小极值 | x | ln(–ln(1 – p)) |
| 最大极值 | x | ln(–ln p) |
| Weibull | ln(x) | ln(–ln(1 – p)) |
| 3 参数 Weibull | ln(x – 阈值) | ln(–ln(1 – p)) |
| 指数 | ln(x) | ln(–ln(1 – p)) |
| 2 参数指数 | ln(x – 阈值) | ln(–ln(1 – p)) |
| 正态 | x | Φ–1norm |
| 对数正态 | ln(x) | Φ–1norm |
| 3 参数对数正态 | ln(x – 阈值) | Φ–1norm |
| Logistic | x |
 |
| 对数 Logistic | ln(x) |
 |
| 3 参数对数 Logistic | ln(x – 阈值) |
 |
| Gamma | x | Φ–1gamma |
| 3 参数 Gamma | ln(x – 阈值) | Φ–1gamma |
注意
由于标绘点并不依赖于任何分布，因此它们对于任意概率图都是一样的（变换前）。但是，拟合线会因所选参数分布的不同而不同。
表示法
| 项 | 说明 |
|---|---|
| p | 估计的概率 |
| Φ-1norm | 标准正态分布的逆 CDF 为 p 返回的值 |
| Φ-1gamma | 不完全 gamma 分布的逆 CDF 为 p 返回的值 |
| ln(x) | x 的自然对数 |
百分位数和百分位数的标准误
百分位数是尺度为 100 的值，表示等于或低于该值的分布的百分比。默认情况下，Minitab 显示百分位表以供对常见百分位数进行参数分布分析。
百分位数的标准误是方差的平方根。
、 
、 
、 
、 
、 
、 
、 
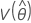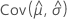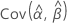和 
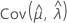表示 μ、σ、α、β、λ 和 θ（从 Fisher 信息矩阵的逆矩阵的相应单元提取）的 MLE 的方差和协方差。
用于百分位数和方差估计值的公式如下所示：
最小极值分布
- 百分位数
-
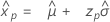
- 方差
-
最大极值分布
- 百分位数
-
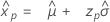
- 方差
-
Weibull 分布
- 百分位数
-
- 方差
-
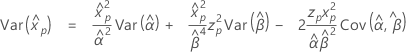
3 参数 Weibull 分布
- 百分位数
-
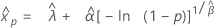
- 方差
-
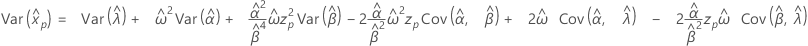
指数分布
- 百分位数
-
- 方差
-
2 参数指数分布
- 百分位数
-
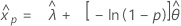
- 方差
-
正态分布
- 百分位数
-
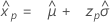
- 方差
-
对数正态分布
- 百分位数
-
- 方差
-
3 参数对数正态分布
- 百分位数
-
- 方差
-
Logistic 分布
- 百分位数
-
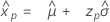
- 方差
-
对数 Logistic 分布
- 百分位数
-
- 方差
-
3 参数对数 Logistic 分布
- 百分位数
-
- 方差
-
Gamma 分布
- 百分位数
-
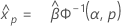
- 方差
-
-
其中，
是规范化不完全 Gamma 分布的逆分布
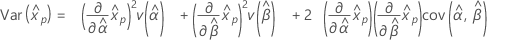
3 参数 Gamma 分布
- 百分位数
-
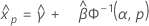
- 方差
-
-
其中，
是规范化不完全 Gamma 分布的逆分布
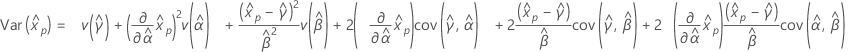
百分位数的置信限
| 分布 | 置信限 |
|---|---|
| 最小极值 |
 |
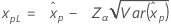| 最大极值 |
 |
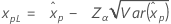| 正态 |
 |
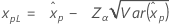| Logistic |
 |
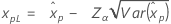| Weibull |
 |
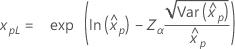| 指数 |
 |
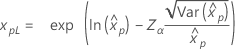| 对数正态 |
 |
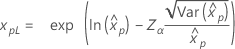| 对数 Logistic |
 |
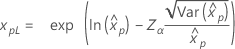| 3 参数 Weibull |
如果 λ < 0：
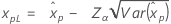 如果 λ ≥ 0：
  |
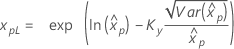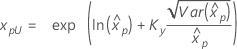| 2 参数指数 |
如果 λ < 0：
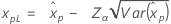 如果 λ ≥ 0：
  |
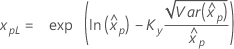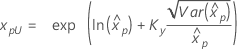| 3 参数对数正态 |
如果 λ < 0：
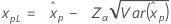 如果 λ ≥ 0：
  |
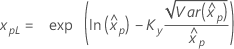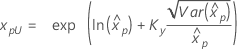| 3 参数对数 Logistic |
如果 λ < 0：
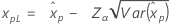 如果 λ ≥ 0：
  |
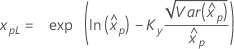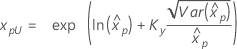表示法
| 项 | 说明 |
|---|---|
| Kγ | 标准正态分布的第 (1 + γ) / 2 个百分位数 |
