N
样本中非缺失值的个数。N 是所有观测值的计数。
| 合计 | N | N* |
|---|---|---|
| 149 | 141 | 8 |
解释
使用 N 估计样本数量。
重要信息
在解释很小或很大样本的结果时请务必谨慎。如果您的样本很小,则拟合优度检验可能没有足够的功效来检测与分布存在显著偏差的情况。如果您的样本很大,则该检验的功效可能很高,从而可以检测到与分布的微小但不具实际意义的偏差。除 p 值以外,还要使用概率图评估分布拟合。
N*
样本中缺失值的个数。N* 是工作表中包含缺失值符号 * 的单元格计数。
| 合计 | N | N* |
|---|---|---|
| 149 | 141 | 8 |
均值
均值是按数据的平均值计算的,它等于所有观测值的和除以观测值的个数。
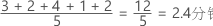
解释
使用均值可以描述使用单个值表示数据中心的样本。许多统计分析都使用均值作为标准参考点。
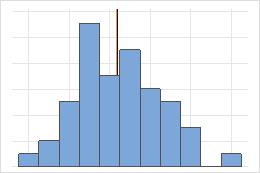
对称分布中的均值和中位数
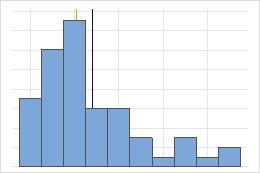
非对称分布中的均值和中位数
对于对称分布,均值(蓝线)和中位数(橙线)几乎相同。因此,这两条线重叠且不能相互区分。对于非对称分布,数据向右偏斜,这会导致均值大于中位数。
标准差
标准差 (StDev) 是离差的最常用度量,即数据围绕均值展开的程度。符号 σ(西格玛)通常用于表示总体的标准差,而 s 用于表示样本的标准差。
解释
使用标准差可以确定数据围绕均值展开的程度。较大样本标准差表示您的数据在均值周围展开得较为广泛。
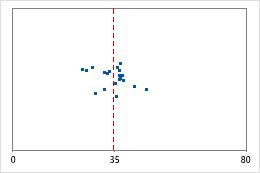
医院 1
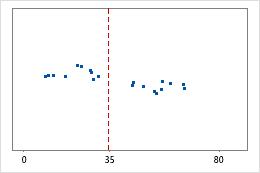
医院 2
医院出院时间
管理员对在两家医院急诊部治疗的患者的出院时间进行跟踪。尽管平均出院时间大致相同(35 分钟),但标准差显著不同。医院 1 的标准差大约为 6。平均而言,患者的出院时间大约偏离均值(虚线)6 分钟。医院 2 的标准差大约为 20。平均而言,患者的出院时间大约偏离均值(虚线)20 分钟。
中位数
中位数是数据集的中点。在此中点值所在的点上,有一半的观测值大于中点值,有一半的观测值小于中点值。中位数是通过对观测值排秩并在秩顺序中查找第 [N + 1] / 2 位的观测值来确定的。如果观测值个数是偶数,则中位数是排在数字 N / 2 处的观测值与排在 [N / 2] + 1 处的观测值之间的值。
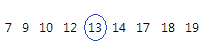
对于此排序数据,中位数是 13。也就是说,一半的值小于或等于 13,一半的值大于或等于 13。
解释

对称分布中的均值和中位数

非对称分布中的均值和中位数
对于对称分布,均值(蓝线)和中位数(橙线)几乎相同。因此,这两条线重叠且不能相互区分。对于非对称分布,数据向右偏斜,这会导致均值大于中位数。
最小值
最小的数据值。
在这些数据中,最小值为 7。
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
解释
使用最小值可以标识可能的异常值。如果值非常低,请调查其可能的原因,如数据输入错误或测量错误。
评估数据散布最简单的方法之一就是比较最小值和最大值以确定其极差。极差是数据集内的最大值和最小值之间的差值。当您评估数据的散布时,还需要考虑其他度量,如标准差。
最大值
最大的数据值。
在这些数据中,最大值为 19。
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
解释
使用最大值可以标识可能的异常值。如果值非常高,请调查其可能的原因,如数据输入错误或测量错误。
评估数据散布最简单的方法之一就是比较最小值和最大值以确定其极差。极差是数据集内的最大值和最小值之间的差值。当您评估数据的散布时,还需要考虑其他度量,如标准差。
偏度
偏度是数据的不对称程度。
解释
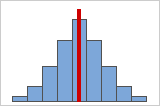
图 A:对称的正态分布数据
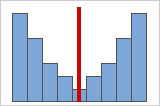
图 B:对称的非正态分布数据
对称或非偏斜分布
数据越对称,它的偏度值越接近 0。图 A 显示正态分布的数据(顾名思义,表现出相对较小偏度的数据)。正态数据直方图中间的线显示两侧相互镜像。但是,本身缺乏偏度并不意味着正态性。图 B 显示两侧相互镜像但数据不呈正态分布的分布。
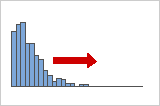
正偏斜或向右偏斜分布
正偏斜数据又称为右偏斜数据,因为分布的“尾部”指向右侧。正偏斜数据具有大于 0 的偏度数据。薪水数据通常是正偏斜的:公司中许多员工的薪水相对较低,而少部分员工的薪水却非常高。
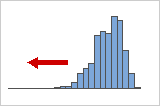
负偏斜或向左偏斜分布
负偏斜数据通常称为左偏斜数据,因为分布的“尾部”指向左侧。负偏斜数据具有小于 0 的偏度值。故障率数据通常是负偏斜的。例如,非常少的灯泡亮一会儿就马上熄灭,大部分灯泡可以长时间不熄灭。
峰度
峰度表示分布的尾部与正态分布的区别。
解释
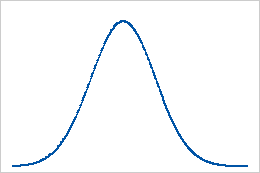
基线:峰度值 0
完全服从正态分布的数据的峰度值为 0。正态分布的数据为峰度建立基准。
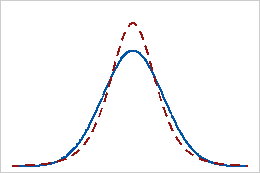
正峰度
具有正峰度值的分布表明,相比于正态分布,该分布有更重的尾部。例如,服从 t 分布的数据具有正峰度值。实线表示正态分布,虚线表示具有正峰度值的 t 分布。
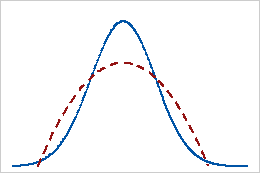
负峰度
具有负峰度值的分布表明,相比于正态分布,该分布有更轻的尾部。例如,服从 Beta 分布(第一个和第二个分布形状参数等于 2)的数据具有负峰度值。实线表示正态分布,虚线表示具有负峰度值的 Beta 分布。
