个体分布标识 示例

解释结果

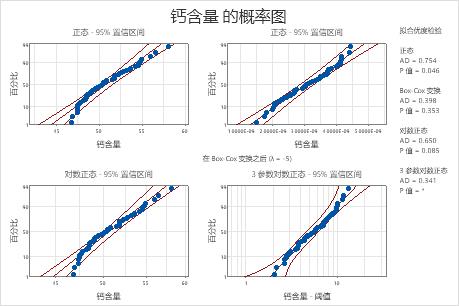
Minitab 对于每个分布和变换显示一个概率图和一个 p 值。如果某个分布能够很好地拟合数据（或者，如果变换有效），则图上的点服从置信界限内的直线，而且 p 值大于 alpha 水平。通常使用 alpha 水平 0.05。似然比检验 (LRT) 的 p 值指示向分布中添加额外参数是否会显著改善拟合优度。小于 0.05 的 LRT p 值表示拟合有显著改善。

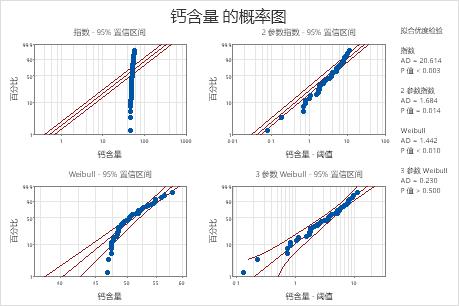
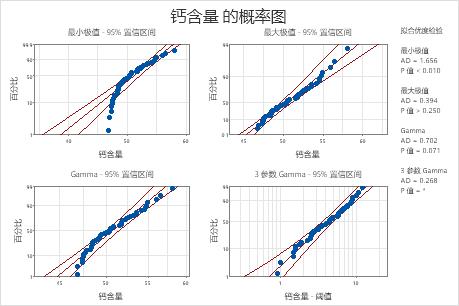
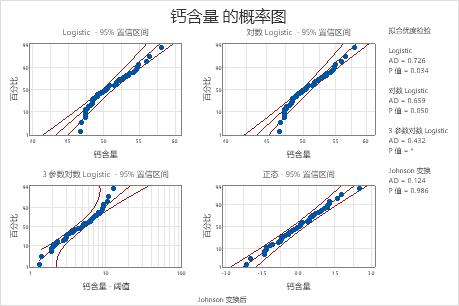
对于这些数据，3 参数 Weibull 分布（P > 0.500）和最大极值分布 (P > 0.250) 能够很好地拟合数据。添加第三个参数会显著改善对数正态分布 (LRT P = 0.017)、Weibull 分布 (LRT P = 0.000)、Gamma 分布 (LRT P = 0.006) 和对数 Logistic 分布 (LRT P = 0.027) 的拟合优度。

Box-Cox 变换 (p = 0.324) 和 Johnson 变换 (p = 0.986) 对于这些数据有效。在变换后，正态分布为变换后的值提供良好的拟合。

描述性统计量

N	N*	均值	标准差	中位数	最小值	最大值	偏度	峰度
50	0	50.782	2.76477	50.4	46.8	58.1	0.644923	-0.287071

Box-Cox 变换: λ = -4

Johnson 变换函数:

0.804604 + 0.893699 × Ln( ( X - 46.2931 ) / ( 59.8636 - X ) )

拟合优度检验

分布	AD	P	极大似然比 P
正态	0.754	0.046
Box-Cox 变换	0.414	0.324
对数正态	0.650	0.085
3 参数对数正态	0.341	*	0.017
指数	20.614	<0.003
2 参数指数	1.684	0.014	0.000
Weibull	1.442	<0.010
3 参数 Weibull	0.230	>0.500	0.000
最小极值	1.656	<0.010
最大极值	0.394	>0.250
Gamma	0.702	0.071
3 参数 Gamma	0.268	*	0.006
Logistic	0.726	0.034
对数 Logistic	0.659	0.050
3 参数对数 Logistic	0.432	*	0.027
Johnson 变换	0.124	0.986

分布参数的极大似然估计

分布	位置	形状	尺度	阈值
正态*	50.78200		2.76477
Box-Cox 变换*	0.00000		0.00000
对数正态*	3.92612		0.05368
3 参数对数正态	1.69295		0.46849	44.74011
指数			50.78200
2 参数指数			4.06326	46.71873
Weibull		17.82470	52.13681
3 参数 Weibull		1.47605	4.53647	46.66579
最小极值	52.22257		2.95894
最大极值	49.50370		2.16992
Gamma		351.04421	0.14466
3 参数 Gamma		2.99218	1.63698	45.88376
Logistic	50.57182		1.59483
对数 Logistic	3.92259		0.03121
3 参数对数 Logistic	1.54860		0.32763	45.46180
Johnson 变换*	0.02897		0.97293