步骤 1:检查评估线性的拟合回归线
线性通过测量系统的预期操作范围评估平均偏倚的差异。
使用“偏倚与参考值”图可以查看每个部件的偏倚值是如何变化的。对于每个参考值,蓝圈表示偏倚值,红色方形表示平均偏倚值。
偏倚是部件参考值和操作员对部件的测量值之间的差异。在“量具偏倚”表的“偏倚”下方还会列出平均偏倚值。
通过偏倚值,利用最小二乘回归法拟合回归线。您希望数据形成水平线,表明偏倚在各个大小部件之间未发生变化,测量系统未包含显著偏倚。当水平线接近于 0 时,观测到的平均测量值和参考值之间的差异会非常小,也表明该系统未包含显著偏倚。
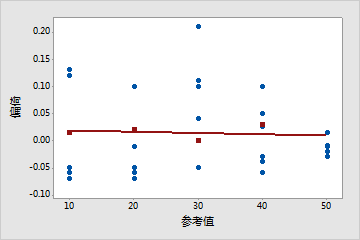
所有部件间的偏倚量很小
理想情况是 — 线为水平线且接近于 0。每个部件的偏倚非常小,水平线表示线性不存在问题。
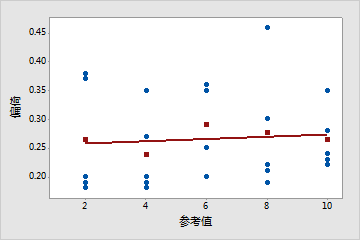
线性看起来没问题
标绘线接近水平,表明平均偏倚相对稳定,且不依赖于参考值。在此示例中,所有部件的测量值高于其相应参考部件的测量值。
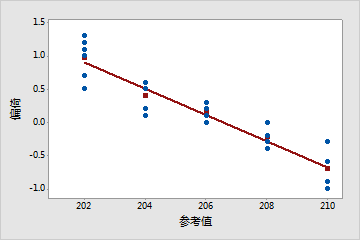
线性看起来有问题
标绘线是倾斜的。在本示例中,较小部件的测量值高于其对应参考部件值的测量值。而较大部件的测量值往往低于其对应参考部件值的测量值。
步骤 2:确定量具线性是否有统计意义
一般而言,拟合线的斜率越接近于零,量具的线性将越好。理想情况下,拟合线将为水平线且接近于 0。
- 如果 p 值大于 0.05,则可以推断线性不存在且可以评估偏倚。使用平均偏倚的 p 值评估平均偏倚是否显著不同于 0。
- 如果 p 值小于或等于 0.05,则可以推断出存在线性问题。您可以评估每个单独参考值的偏倚而非整体偏倚。当存在显著线性时将无法评估整体偏倚,因为不同参考值上的偏倚是不同的。换句话说,当线性具有显著统计意义时,将仅解释单个参考水平的偏倚 p 值。
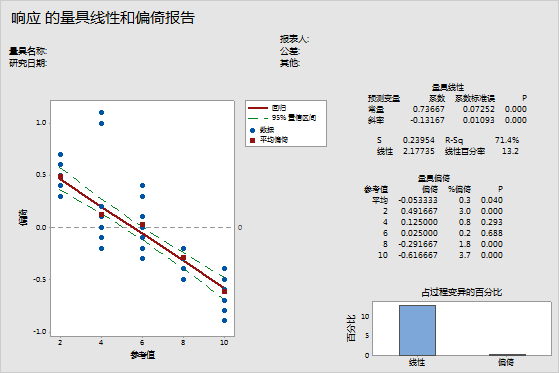
主要结果:量具线性 P
在这些结果中,斜率的 p 值是 0.000,表明斜率是显著的,且在测量系统中存在线性。因为线性具有显著统计意义,您必须使用单个偏倚值而不能使用整个平均偏倚值。
步骤 2:确定比值在统计意义上是否显著
偏倚是部件的参考值与操作员的部件测量值之差。检查每个参考值的偏倚百分比和平均偏倚百分比。平均偏倚百分比是表示为过程变异性百分比的偏倚。
- 正偏倚表示量具测量值高。
- 负偏倚表示量具测量值低。
对于可以准确测量的量具,偏倚百分比值也很小。
使用 P 值可以检验对于每个参考值和平均值偏倚是否有偏倚 = 0。

主要结果:偏倚百分比、量具偏倚 P
在这些结果中,偏倚百分比值的范围是 0.2 到 3.7,其 P 值的范围是 0.000 到 0.688。由于存在线性,因此仅解释单个参考水平的偏倚 p 值,而不使用总体平均偏倚值。参考值 2、8 和 10 的测量值有偏倚,而参考值 4 和 6 的测量值似乎没有偏倚。
