偏倚与参考图
使用“偏倚与参考”图可以查看每个部件的偏倚值是如何变化的。蓝点表示每个参考值的偏倚值。红色方框表示每个参考值的平均偏倚值。直线表示拟合偏差的平均值的最小二乘回归线。
解释
理想情况下,每个部件的偏差接近于 0 且此拟合线为水平线。
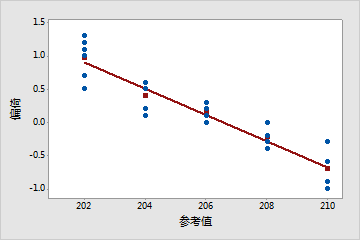
线性看起来有问题
标绘线是倾斜的。在本示例中,较小部件的测量值高于其对应参考部件值的测量值。而较大部件的测量值往往低于其对应参考部件值的测量值。
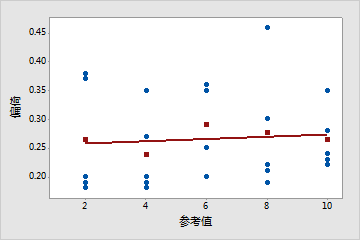
线性看起来没问题
标绘线接近水平,表明平均偏倚相对稳定,且不依赖于参考值。在此示例中,所有部件的测量值高于其相应参考部件的测量值。
系数
系数是一些来自偏倚与参考值图的回归线的数字。
此最小二乘回归线的一般形式为:
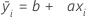
项 b 表示固定系数。它表示拟合线与 Y 轴的相交位置。
项 a 表示斜率系数。直线的斜率表示直线的陡峭程度,是 Y 轴随 X 轴变化所发生的变化情况。
解释
当斜率系数 a 非常小时,斜率接近于水平。因此,偏倚在多个参考值之间相对稳定,其线性不是显著问题。斜率系数的绝对值 |a| 越大,表示直线的陡峭斜率越大。如果斜率的 p 值小于 alpha,则线性显著。
如果没有显著线性,则固定常量的绝对值 |b| 越大,表示偏倚越大。如果有显著线性,则必须查看各个偏倚值。
系数标准误
回归系数估计值的标准误度量模型对系数未知值的估计的精确度。系数的标准误始终为正。
解释
使用系数的标准误来度量系数估计值的精确度。标准误越小,估计值越精确。将系数除以其标准误计算 t 值。如果与此 t 值关联的 p 值小于 α 水平,则断定系数显著不等于零。
量具线性的 p 值
- 常量的 p 值:用于检验线性直线的常量是否等于 0。
- 斜率的 p 值:用于检验线性直线的斜率是否等于 0。
解释
- 对于常量,如果 p 值大于 α 值,则不能否定原假设,并得出所有参考值的偏倚量等于 0 的结论。
- 对于斜率,如果 p 值大于 α 值,则不能否定原假设,并得出测量系统对于所有的参考值具有相同的偏倚量(不存在线性)的结论。
- 对于常量,如果 p 值小于 α 值,则可否定原假设,并得出所有参考值的偏倚量不等于 0 的结论。
- 对于斜率,如果 p 值小于 α 值,则可否定原假设,并得出测量系统对于所有的参考值不具有相同的偏倚量(存在线性)的结论。
S 和 R 平方
S 和 R 平方 (R2) 是模型对数据的拟合优度的度量。
S 是对 σ 估计,是围绕回归线的标准差。
R 平方 (R2) 表示偏倚中的变异部分,依据偏倚和参考值之间的线性关系进行解释。
解释
S 值越小表示在偏倚估计中的变异越少。R2 介于 0 和 100% 之间。通常,R2 值越高,模型拟合数据的优度越高。
线性、线性百分比
线性通过测量系统的预期操作范围评估平均偏倚的差异。线性指示您的量具是否在所有参考值中具有相同的准确性(相同偏倚)。
线性百分比是线性表示为过程变异的百分比。
解释
要解释数据的线性,需要确定参考值中的偏倚是否有变化。如果数据没有在散点图上形成一条水平线,则表明存在线性。理想情况下,拟合线应为水平线,且接近于 0。

线性看起来有问题
标绘线是倾斜的。在本示例中,较小部件的测量值高于其对应参考部件值的测量值。而较大部件的测量值往往低于其对应参考部件值的测量值。

线性看起来没问题
标绘线接近水平,表明平均偏倚相对稳定,且不依赖于参考值。在此示例中,所有部件的测量值高于其相应参考部件的测量值。
对于连续度量不同部件的量具,线性百分比将接近于 0。
偏倚、%偏倚
偏倚等于参考部件的已知标准值与观测到的平均测量值之间的差异。偏倚用来度量测量系统的准确度。
%偏倚是表示为过程变异性的百分比。
解释
- 正偏倚表示量具测量值高。
- 负偏倚表示量具测量值低。
对于可以准确测量的量具,偏倚百分比将很小。
量具偏倚的 p 值
- 平均值偏倚的 P 值:用于检验平均值偏倚是否等于 0。
- 每个参考值的 p 值:用于检验每个参考值上的偏倚是否等于 0。
解释
- 对于每个参考值,如果 p 值大于 α 值,您将无法拒绝原假设,并得出结论:偏倚等于 0。
- 对于平均值偏倚,如果 p 值大于 α 值,则将拒绝原假设,并得出结论:平均偏倚等于 0。
- 对于每个参考值,如果 p 值小于 α 值,则将拒绝原假设,并得出结论:偏倚不等于 0。
- 对于平均值偏倚,如果 p 值小于 α 值,则将拒绝原假设,并得出结论:平均偏倚不等于 0。
