扩展量具 R&R 研究示例

某工艺工程师想要评估用于玻璃生产过程的玻璃折射测量系统。这位工程师让三名操作员在两个站点测量了 22 个玻璃部件的折射属性。

由于此研究具有固定因子（站点），因此，此工程师想要执行扩展量具 R&R 研究来评估因测量系统导致的测量值的变异性。

打开样本数据，玻璃折射.MWX.
选择统计 > 质量工具 > 量具研究 > 量具 R&R 研究（扩展）。
在部件号中，输入部件。
在操作员中，输入操作员。
在测量数据中，输入测量。
在附加因子中，输入站。
在固定因子中，输入站。
单击项按钮。
从按顺序在模型中包括项，选择 2。
在选定项下，从模型删除部件*服务站交互作用项。
在每个对话框中单击确定。

解释结果

第一个双因子方差分析表包含部件、操作员、固定因子和交互作用的项。如果交互作用的 p 值 ≥ 0.05，Minitab 将忽略来自全模型的交互作用，因为该交互作用不是显著性的。在此示例中，部件*操作员的 p 值等于 0.189，操作员*服务站的 p 值等于 0.598。因此，Minitab 将再生成一个双因子方差分析表，该分析表将忽略最终模式中的这些交互作用。

对于折射数据，测量系统（合计量具 R&R 贡献百分比约为 49%）具有与部件（部件间的贡献百分比约为 51%）一样多的变异。合计量具 R&R 大致为研究变异的 70%。重复性约为研究变异的 69%，该值说明测量系统测量同一部件时结果不一致。

此过程仅可以区分 1 种可区分类别，说明测量系统不能区分部件。有关详细信息，请转到在量具 R&R 研究中使用不同类别的数量。

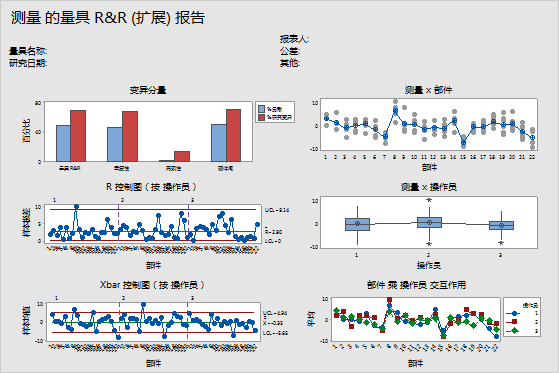
此图还提供了有关测量系统的以下信息：

在变异分量图中，您可以看到测量系统解释与部件间变异一样多的变异。特别是，绝大部分变异性是由测量系统的不准确造成的（重复性）。
在“R 控制图（按操作员）”中，一些数据点不在控制范围内，说明三个操作员的测量结果不一致。
在“Xbar 控制图（按操作员）”中，每个操作员仅有几个数据点在控制范围之外。对于此控制图，应至少有 50% 的数据点在控制范围之外以说明系统是可接受的测量系统。因此，在此示例中，Xbar 控制图表明此测量系统可能不是可接受的测量系统。
在“按部件”图中，每个部件的测量值显著不同。此变异性可能是由于测量系统不准确造成的。平均值也显著不同，这种情况极有可能是因为此研究中使用的部件应代表所有可能的部件。
在“操作员对比图”中，每个操作员的测量值之间的差值应近似相等。在始终存在一些变异的情况下，该数据说明操作员测量各部件的结果类似。
在“操作员*部件交互作用”图中，所有线的形状都非常相似。但是，也存在一些不一致。例如，操作员 3 似乎对部件 19 的测量与其他两位操作员的测量值不同。

因子信息

因子	类型	水平数	值
部件	随机	22	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22
操作员	随机	3	1, 2, 3
站	固定	2	1, 2

具有所有项的方差分析表

来源	自由度	Seq SS	Adj SS	Adj MS	F 值	P 值
部件	21	1071.30	1071.30	51.014	6.46	0.000
操作员	2	32.18	32.18	16.089	3.27	0.164	x
站	1	11.25	11.25	11.247	3.50	0.202
部件*操作员	42	331.81	331.81	7.900	1.27	0.189
操作员*站	2	6.43	6.43	3.217	0.52	0.598
重复性	63	390.53	390.53	6.199
合计	131	1843.50

具有用于量具 R&R 计算的项的方差分析表

来源	自由度	Seq SS	Adj SS	Adj MS	F 值	P 值
部件	21	1071.30	1071.30	51.014	7.49	0.000
操作员	2	32.18	32.18	16.089	2.36	0.099
站	1	11.25	11.25	11.247	1.65	0.202
重复性	107	728.77	728.77	6.811
合计	131	1843.50

方差分量

来源	方差分量	方差分量贡献率
合计量具 R&R	7.1070	49.10
重复性	6.8109	47.06
再现性	0.2961	2.05
操作员	0.2109	1.46
站	0.0852	0.59
部件间	7.3672	50.90
部件	7.3672	50.90
合计变异	14.4743	100.00

量具评估

来源	标准差(SD)	研究变异 (6 × SD)	%研究变异 (%SV)
合计量具 R&R	2.66590	15.9954	70.07
重复性	2.60978	15.6587	68.60
再现性	0.54413	3.2648	14.30
操作员	0.45921	2.7552	12.07
站	0.29189	1.7514	7.67
部件间	2.71427	16.2856	71.34
部件	2.71427	16.2856	71.34
合计变异	3.80450	22.8270	100.00

可区分的类别数 = 1