方差分量
方差分量的贡献图和方差分量表显示了不同来源的方差。
解释
使用方差分量评估每个源的方差。重测方差和算子方差是测量误差。部件变体表示算例中部件的范围。总方差是其他分量的总和。如果分析包括交互作用,则测量误差的大小取决于操作员测量的零件。
在可接受的测量系统中,最大的变化分量是零件变化。如果重测变异和算子变异导致了大量变异,请调查问题的根源并采取纠正措施。
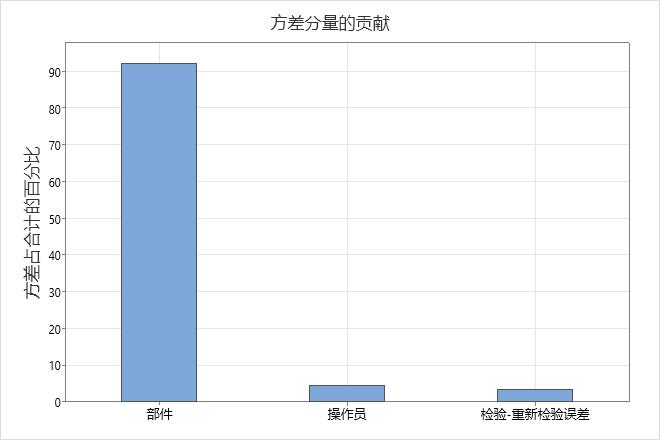
方差分量
| 来源 | 方差 | %合计 | 标准差 |
|---|---|---|---|
| 检验-重新检验误差 (重复性) | 0.03997 | 3.394 | 0.19993 |
| 操作员(再现性) | 0.05146 | 4.368 | 0.22684 |
| 部件(产品变异) | 1.08645 | 92.238 | 1.04233 |
| 合计 | 1.17788 | 100.000 | 1.08530 |
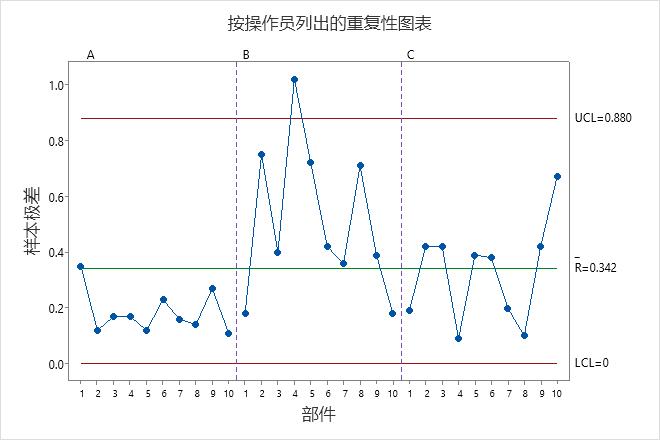
重复性图表
重复性图表是显示操作员一致性的范围控制图。
- 标绘点
- 对于每个操作员,采样范围是每个零件的最大和最小测量值之间的差值。使用采样范围来评估运算符的一致性。
- 中心线 (Rbar)
- 过程的总平均值(即所有样本极差的平均值)。
- 控制限(LCL 和 UCL)
- 预计的样本极差变异量。Minitab 使用样本内的变异计算控制限。
注意
如果每个操作员测量每个部件 9 次或更多次,Minitab 将在图表上显示标准差而不是范围。
解释
平均范围越小,与测量系统的变化就越小。高于控制上限 (UCL) 的点表示操作员对部件的测量不一致。UCL 的计算包括每个操作员对每个零件的测量次数和零件变化。如果操作员对部件的测量一致,那么与研究变异相比,最高测量值与最低测量值之间的极差就很小,且各个点都应该处于受控状态。
运营商的信噪比图表
该图表将部件变体与重测组件进行比较。
- 标绘点
- 每个部件的平均测量值,由每位操作员标绘。
- 中心线 (
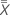 )
) - 所有操作员测量的所有部件测量值的整体平均值。
- 控制限(LCL 和 UCL)
- 控制限基于每个平均值中的重复性估计和测量次数。
解释
为研究选择的零件应代表可能零件的整个范围。因此,该图应指示零件平均值之间的变异大于仅重测变异的预期。
通常,该图的控制限较窄,其中的许多失控点表示具有低变异的测量系统。
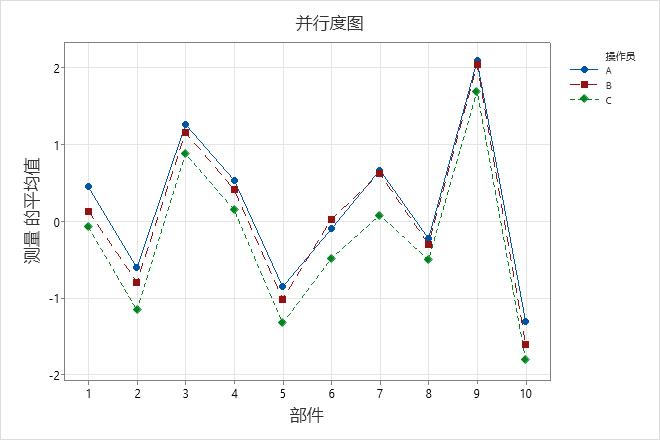
并行度图
平行度图显示每个操作员对每个零件的平均测量值。每条连接线代表每个操作员的测量均值。
该图显示了两个变异源之间的相互作用:部件和操作员。当某一因子的效应取决于另一因子时就会发生交互作用。
解释
线重合在一起表示操作员的测量结果相似。线交叉在一起或者不平行表示操作员一致地测量部件的能力取决于测量哪个部件。如果一条线始终高于或低于其他线,则表示操作员的测量值始终偏高或低,这会为测量值增加偏倚量。
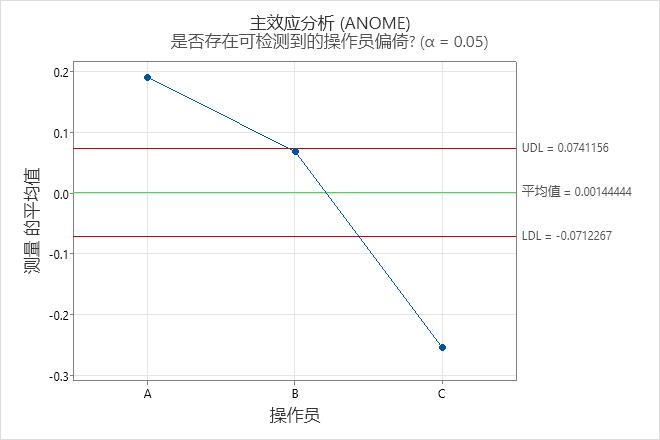
主效应分析(ANOME)图
该图比较了算子的平均测量值。
- 标绘点
- 每个操作员所有零件的平均测量值。
- 中心线(平均)
- 所有操作员测量的所有部件测量值的整体平均值。
- 决策限制(LDL 和 UDL)
- 这些限制基于重测估计值和每个平均值中的测量值。
解释
超出决策限的点表明不同的算子会给测量增加偏差。理想情况下,这些点都在决策限内,以指示运算符的总体平均值相似。
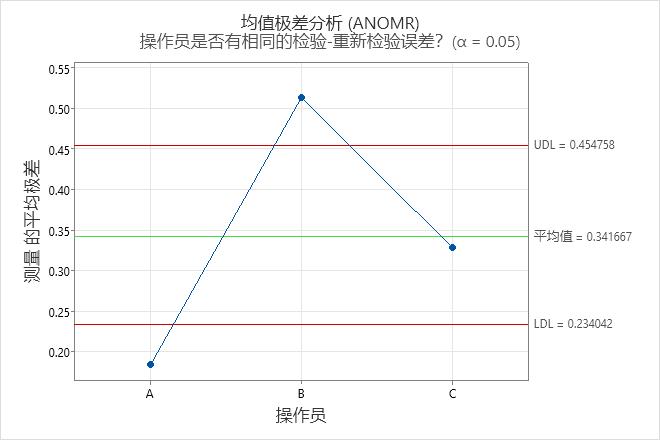
均值极差分析 (ANOMR) 图
该图比较了算子的平均测量范围。
- 标绘点
- 每个操作员的每个零件的测量范围的平均值。
- 中心线(平均)
- 所有运营商所有范围的总体平均值。
- 决策限制(LDL 和 UDL)
- 这些限制基于重测估计值。
解释
超出决策限的点表明,某些算子的测量结果或多或少比其他算子一致。理想情况下,这些点都在决策限内,以指示运算符的总体范围相似。
EMP 统计和分类指南
EMP 统计数据将测量系统从一等舱的最佳评级到四等舱的最差评级进行分类。这些类对应于类内相关系数。实际上,该系数解释了测量系统检测到至少 3 个标准差的过程均值偏移的程度。一等和二等测量系统通常很有可能通过控制图上有限数量的测试和子组来检测此类偏移。对于第三类测量系统,典型分析将检验添加到控制图中,以增加检测到过程均值偏移的概率。第四类测量系统通常需要改进以监控过程或过程改进活动。
该分类还与来自过程的信号衰减有关。衰减是与测量误差混淆的变化量。对于衰减 50% 变化的测量系统,2 个标准差的变化很可能显示为 1 个标准差的变化。
- 重测错误
- 当同一操作员多次测量同一零件时,测量结果的可变性。该值越小,测量系统的性能越好。
- 自由度
- 用于估计重测误差的自由度 (DF)。通常,DF 测量可用于计算误差的信息量。
- 或然误差
- 单次测量的不确定度。该分析将可能的误差与“测量的有效分辨率”表中的测量增量进行比较,以得出测量精度是否可信的结论。 Wheeler (2006) 1 描述在给定测量系统性能的情况下,使用可能误差确定过程的规格限值的方法。
- 类内相关
- 组内相关系数将总变异与部分变异进行比较。值越接近 1,表示与测量系统的变化越小。
- 无偏见
- 在没有偏差的情况下,该系数描述了如果所有操作员平均测量零件相同,测量系统的性能如何。
- 带偏倚
- 对于偏差,该系数描述了测量系统在操作员之间存在差异时的性能。
- 带偏倚和交互作用
- 当分析检测到不同的操作员以不同的方式测量不同的零件时,结果包括与偏差和交互作用的组内相关性。该系数描述了当不同的操作员以不同的方式测量不同零件时,测量系统的性能。
- 偏倚影响
- 有偏差和无偏差的类内系数之间的差异。该值越小,算子差异对测量值变化的影响就越小。
- 偏倚和交互作用影响
- 具有偏差和交互作用的类内系数与无偏差系数之间的差异。该值越小,不同操作员测量不同零件的方式差异对测量变化的影响就越小。
EMP 统计量
| 统计量 | 值 | 分类 |
|---|---|---|
| 检验-重新检验误差 | 0.1999 | |
| 自由度 | 78.0000 | |
| 或然误差 | 0.1349 | |
| 类内相关(无偏倚) | 0.9645 | 第一类 |
| 类内相关(带偏倚) | 0.9224 | 第一类 |
| 偏倚影响 | 0.0421 |
分类准则
| 分类 | 类内相关 | 过程信号衰减 | 警告概率,检验 1* | 警告概率,检验* |
|---|---|---|---|---|
| 第一类 | 0.80 - 1.00 | 小于 11% | 0.99 - 1.00 | 1.00 |
| 第二类 | 0.50 - 0.80 | 11 - 29% | 0.88 - 0.99 | 1.00 |
| 第三类 | 0.20 - 0.50 | 29 - 55% | 0.40 - 0.88 | 0.92 - 1.00 |
| 第四类 | 0.00 - 0.20 | 大于 55% | 0.03 - 0.40 | 0.08 - 0.92 |
测量值的有效分辨度
有关分辨率的统计数据描述了您可以信任测量记录的精度的程度。
- 或然误差 (PE)
- 单次测量的不确定度。该分析将可能的误差与“测量的有效分辨率”表中的测量增量进行比较,以得出测量精度是否可信的结论。Wheeler (2006)1 描述了在给定测量系统性能的情况下,使用可能误差来确定过程规格限值的方法。
- 增量下限 (0.1 * PE)
- 当测量增量可信时的下限。当测量增量小于增量的下限时,强烈考虑是否以较低的精度记录测量值。
- 最小有效增量 (0.22 * PE)
- 对系统可能产生的测量精度的估计。当测量增量小于最小有效增量时,请考虑是否以较低的精度记录测量值。
- 当前测量值增量
- 根据数据或指定值进行估计,用于解释记录的测量值的精确程度。例如,对于值 1.1、1.4 和 1.9,分析确定增量为 0.1,因为测量值包括十分之一位。
- 最大有效增量 (2.2 * PE)
- 对系统可能产生的测量精度的估计。当测量增量大于最大有效增量时,请考虑是否更精确地记录测量值。
误分类的概率
当您指定至少一个规格限时,Minitab 可以计算将产品误分类的概率。由于量具的变化,零件的测量值并不总是等于零件的真实值。测量值与实际值之间的差异可能会对零件进行错误分类。
- 联合概率
- 当您对零件的可接受性没有先验知识时,请使用联合概率。例如,您正在生产线中抽样,但并不了解具体每个部件合格与否。您可以进行两种错误分类:
- 部件不合格而您接受其的概率。
- 部件合格但您拒绝其的概率。
- 条件概率
- 当您对部件的可接受性有先验知识时,请使用条件概率。例如,您正在从一堆返工品中或从即将作为合格产品发货的一批产品中抽样。您可以进行两种错误分类:
- 您接受从一堆需要返工的不良产品中抽样的部件的概率(也称为错误接受)。
- 拒收从一堆即将发货的优质产品中抽样的部件的概率(也称为错误拒收)。
解释
误分类的联合概率
| 说明 | 概率 |
|---|---|
| 随机选择的部件不合格,但被接受 | 0.037 |
| 随机选择的部件合格,但被拒绝 | 0.055 |
误分类的条件概率
| 说明 | 概率 |
|---|---|
| 来自一组不合格产品的部件被接受 | 0.151 |
| 来自一组合格产品的部件被拒绝 | 0.073 |
一个零件是坏的,而你接受它的联合概率是 0.037。一个零件是好的,而你拒绝它的联合概率是 0.055。
错误验收的条件概率为 0.151,即在重新检查期间接受确实超出规格的零件。错误剔除的条件概率为 0.073,即在重新检查期间拒绝的零件,而该零件确实符合规格。
