G 控制图的方法和公式

请选择您所选的方法或公式。

关于本主题

标绘点
中心线和控制限
特殊原因检验（包括 Benneyan 检验）

标绘点

如果数据以每个事件的日期形式记录，则每个标绘点 x_i 表示连续事件之间的天数。如果数据以事件之间的机会数形式记录，则每个标绘点表示连续事件之间的机会数。

中心线和控制限

中心线 (CL)

中心线是分布的第 50 个百分位数。中心线等于 G2 – 1。

注意

之所以减去 1，是因为 Minitab 在其计算中使用几何分布的“之前数量”定义，但是 G 控制图上标绘的是“之间数量”值。

G2 等于具有参数 p 的几何分布的 INVCDF (.5)。

Minitab 给出 G2_a 和 G2_b (G2_a = G2_b – 1) 两个值，以及 p2_a 和 p2_b (p2_a < p2_b) 两个概率。使用简单线性插值时，G2 = G2_a + (..5 – p2_a) / (p2_b – p2_a)。

控制下限 (LCL)

LCL = G1 – 1

G1 等于具有参数 p 的几何分布的 INVCDF (..00135)。

Minitab 给出 G1_a 和 G1_b (G1_a = G1_b – 1) 两个值，以及 p1_a 和 p1_b (p1_a < p1_b) 两个概率。使用简单线性插值时，G1 = G1_a + (.00135 – p1_a) / (p1_b – p1_a)。

控制上限 (UCL)

UCL = G3 – 1

G3 等于具有参数 p 的几何分布的 INVCDF (..99865)。

Minitab 给出 G3_a 和 G3_b (G3_a = G3_b – 1) 两个值，以及 p3_a 和 p3_b (p3_a < p3_b) 两个概率。使用简单线性插值时，我们获得 G3 = G3_a + (..99865 – p3_a) / (p3_b – p3_a)。

表示法

项	说明
N	用在计算中的数据值数量（如果数据是日期，则减去 1，因为 Minitab 绘制的是差值。）
	标绘点的平均值
事件概率 (p)

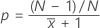特殊原因检验（包括 Benneyan 检验）

检验 1−4

检验 1 基于几何分布。检验 2、3 和 4 与属性控制图中使用的检验相同。

如果 K = 3，则用于控制限的 G1 和 G3 值会定义检验 1 的故障。如果 K 小于或大于 3，则 G1' 下方的标绘点在检验 1 中失败，G3' 上方的标绘点在检验 1 中失败。

G1 = 具有参数 p 的几何分布的 INVCDF (0.00135)
G3 = 具有参数 p 的几何分布的 INVCDF (0.99865)；标绘点的平均值
G1' = 具有参数 p 的几何分布的 INVCDF (p1')
G3' = 具有参数 p 的几何分布的 INVCDF (p2')
p1' = 均值为 0 且标准差为 1 的正态分布的 CDF (–K)
p2' = 均值为 0 且标准差为 1 的正态分布的 CDF (K)

Benneyan 检验

Benneyan 检验使用以下公式对等于控制下限的连续标绘点的数量进行计数以生成信号：

Minitab 将 cp 向上取整到下一个整数，并使用该值作为生成信号所必需的、等于控制下限的连续标绘点的数量。

有关 Benneyan 检验的更多信息，请参见 Benneyan¹ 。

表示法

项	说明
CDF()	均值为 0 且标准差为 1 的正态分布的 CDF
k	检验 1 的参数。默认值为 3。

¹ J. C. Benneyan (2001)。“Performance of Number-Between g-Type Statistical Control Charts for Monitoring Adverse Events”（用来监视不利事件的 g 型统计控制图之间数量的性能），Health Care Management Science（医疗保健管理科学），第 4 期，第 319 到 336 页

G 控制图 的方法和公式