当您在 Minitab 中执行非正态能力分析时,默认情况下将使用 Z 值法计算正态能力指标。
转换规格限
要计算 Z 值,Minitab 首先根据您为分析指定的非正态分布确定超出规格限的观测值的比率。
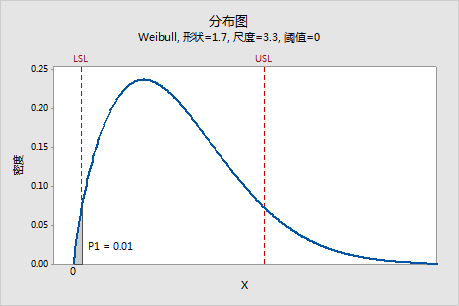
此图中的阴影区域代表 P1,这是测量值 X 小于规格下限 (LSL) 的概率(使用为分析指定的非正态分布)。在此示例中,指定的非正态分布为 Weibull,参数是从数据中估计的,且 P1 = 0.01。
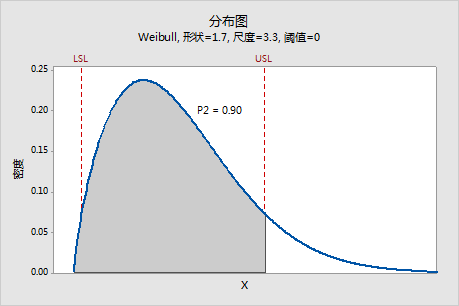
此图中的阴影区域代表 P2,这是测量值 X 小于规格上限 (USL) 的概率(使用为分析指定的非正态分布)。在此示例中,指定的非正态分布为 Weibull,参数是从数据中估计的,且 P2 = 0.90。
然后,使用概率 P1 和 P2 计算标准正态分布的对应 Z 值。使用这种方式,原始规格限可由标准正态尺度上的对应 Z 值表示。
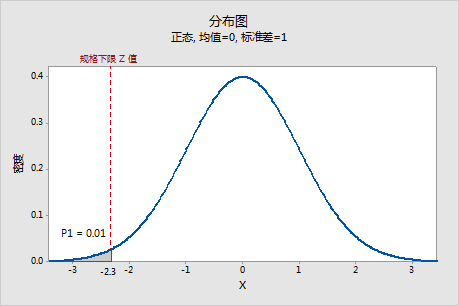
当 P1 在标准正态分布上表示时,由 P1 确定的相应 Z 值称为 Z.LSL,这是标准正态尺度的规格下限。在此示例中,Z.LSL 约为 -2.3。
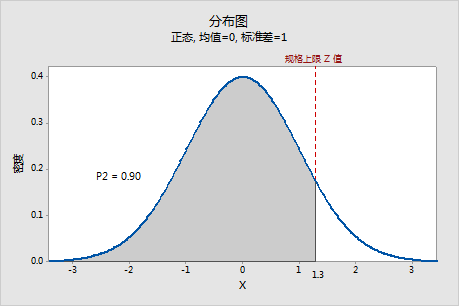
当 P2 在标准正态分布上表示时,由 P2 确定的相应 Z 值称为 Z.USL,这是标准正态尺度的规格上限。在此示例中,Z.USL 约为 1.3。
要确定标准正态分布中的规格展开,需从 Z.USL 的值中减去 Z.LSL 的值。
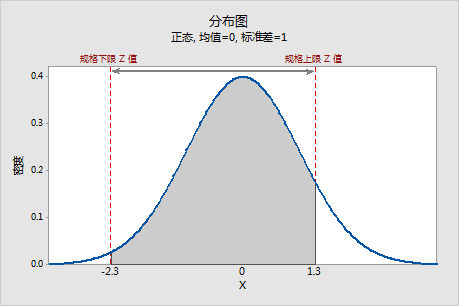
在此示例中,规格展开为 1.3 - (−2.3) = 3.6,如箭头所示。
计算非正态能力指标
然后,根据标准正态规格展开与特定标准正态分布展开之间的关系计算整体能力指标。
Pp 是标准正态规格展开与 6-sigma 展开 (6) 的比率,其从标准正态分布中捕获 99.74% 的过程测量值。
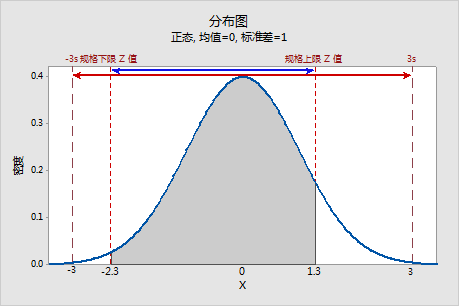
在此示例中,Pp 等于 3.6/6 ≈ 0.6。
PPL 是相对于规格下限 (Z.LSL) 的单侧规格展开与 6-sigma 展开的一半 (3) 的比率。
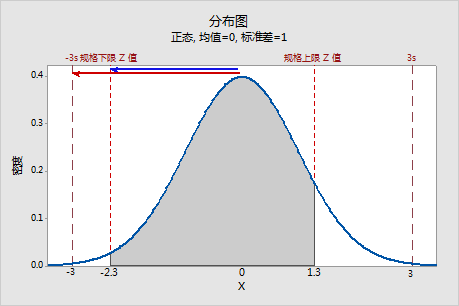
在此示例中,PPL 等于 −2.3/-3 ≈ 0.76。
PPL 是相对于规格上限 (Z.USL) 的单侧规格展开与 6-sigma 展开的一半 (3) 的比率。
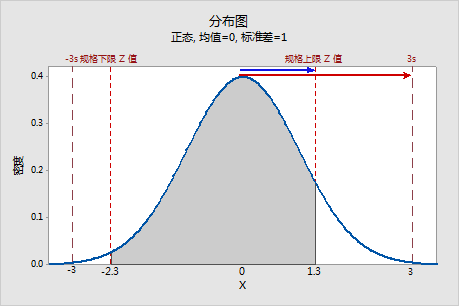
在此示例中,PPU 等于 1.3/3 ≈ 0.43。
Ppk 是 PPU 和 PPL 中的最小值。因此,在此示例中,Ppk 等于 PPU ≈ 0.43。
