关于本主题
估计标准差
组间/组内能力分析基于以下四个标准差:
子组内标准差
σ组内 是子组内变异的估计值(例如,一个班次、一个操作员或一个材料批次)。Minitab 使用以下方法之一估计 σ组内:
- 合并标准差:

其中:
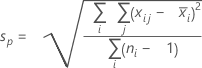
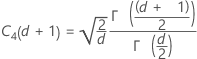
注意
如果更改了默认方法,并且选择不使用无偏常量,将根据 Sp 估计 σ组内。
项 说明 d Sp 的自由度 = Σ (ni- 1) Xij 第 i 个子组中的第 j 个观测值 X̅i 第 i 个子组的均值 ni 第 i 个子组中的观测值个数 C4(d+1) 无偏常量 Γ(·) Gamma 函数 - 子组极差平均值 (Rbar):

其中:
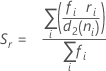
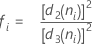
如果 n 都相同:
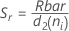
项 说明 ri 第 i 个子组的极差 d2 (ni) 从表中读取的无偏常量(有关更多信息,请参见无偏常量 d2()、d3() 和 d4() 部分) d3 (ni) 从表中读取的无偏常量(有关更多信息,请参见无偏常量 d2()、d3() 和 d4() 部分) ni 第 i 个子组中的观测值个数 - 子组标准差平均值 (Sbar):

其中:
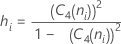
注意
如果更改了默认设置,并且不使用无偏常量,将根据 Σ Si/子组数量估计 σ组内。
项 说明 C4(ni) 无偏常量(为合并标准差所定义) Si 子组 i 的标准差 ni 第 i 个子组中的观测值个数
子组间标准差
σ组间 是子组间变异的估计值(例如,在设定的区间、批次中收集的子组,或由不同的操作员收集的子组)。
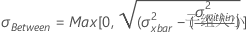
- 移动极差平均值:
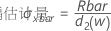
其中:

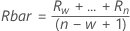
项 说明 Ri 第 i 个移动极差 w 在移动极差中使用的观测值个数。默认值为 w = 2。 d2(w) 从表中读取的无偏常量(有关更多信息,请参见无偏常量 d2()、d3() 和 d4() 部分) - 移动极差中位数:
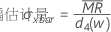
其中:

项 说明 MRi 第 i 个移动极差 
MRi 的中位数 w 在移动极差中使用的观测值个数。默认值为 w = 2。 d4(w) 从表中读取的无偏常量(有关更多信息,请参见无偏常量 d2()、d3() 和 d4() 部分) - 递差均方和平方根 (MSSD):
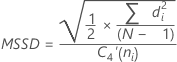
注意
如果更改默认设置,而又不使用无偏常量,将根据以下公式估计 σ组内:

项 说明 di 递差组均值 C4(ni) 无偏常量(为合并标准差所定义) C4'(ni) 无偏常量 ≈ c4(ni)。有关详细信息,请参见“无偏常量 c4'()”部分。 N 观测值总数 ni 第 i 个子组中的观测值个数
组间/组内标准差

| 项 | 说明 |
|---|---|
| σ2组间 | 子组间方差 |
| σ2组内 | 子组内方差 |
整体标准差

其中:
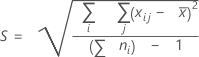
注意
默认情况下,Minitab 在估计 σ整体 时不使用无偏常量。σ整体 用 S 来估计。如果要使用无偏常量来估计整体标准差,则可以在执行能力分析时更改估计子对话框上的此选项。如果希望 Minitab 在默认情况下始终使用无偏常量,请选择,然后选择相应选项。
| 项 | 说明 |
|---|---|
| Xij | 第 i 个子组中的第 j 个观测值 |
| X̅ | 过程均值 |
| ni | 第 i 个子组中的观测值个数 |
| C4 (N) | 无偏常量(为合并标准差所定义) |
| N(或 Σ ni) | 观测值总数 |
Box-Cox 变换
Box-Cox 变换估计 lambda 值(如下表所示),该值最小化标准式变换的变量的标准偏差。由此生成的变换是 Yλ(当 λ ҂ 0 时)及 ln Y(当 λ = 0时)。
Box-Cox 方法通过多种变换类型进行搜索。下表显示了一些常见的变换,其中 Y' 是数据 Y 的变换。
| Lambda (λ) 值 | 变换 |
|---|---|
 |
 |
 |
 |
 |
 |
 |
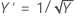 |
 |
 |
