估计标准差
正态能力分析估计子组内标准差和整体标准差。
子组内标准差
用于估计 σwithin 的方法取决于子组大小。
- 合并标准差:

其中:
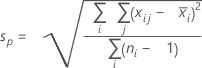
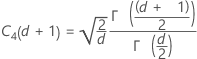
注意
如果更改了默认方法,并且选择不使用无偏常量,将根据 Sp 估计 σ组内。
项 说明 d Sp 的自由度 = Σ (ni- 1) Xij 第 i 个子组中的第 j 个观测值 X̅i 第 i 个子组的均值 ni 第 i 个子组中的观测值个数 C4(d+1) 无偏常量 Γ(·) Gamma 函数 - 子组极差平均值 (Rbar):

其中:
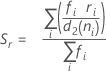
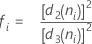
如果 n 都相同:
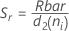
项 说明 ri 第 i 个子组的极差 d2 (ni) 从表中读取的无偏常量(有关更多信息,请参见无偏常量 d2()、d3() 和 d4() 部分) d3 (ni) 从表中读取的无偏常量(有关更多信息,请参见无偏常量 d2()、d3() 和 d4() 部分) ni 第 i 个子组中的观测值个数 - 子组标准差平均值 (Sbar):

其中:
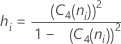
注意
如果更改了默认设置,并且不使用无偏常量,将根据 Σ Si/子组数量估计 σ组内。
项 说明 C4(ni) 无偏常量(为合并标准差所定义) Si 子组 i 的标准差 ni 第 i 个子组中的观测值个数
- 移动极差平均值:

其中:

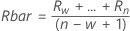
项 说明 Ri 第 i 个移动极差 w 在移动极差中使用的观测值个数。默认情况下,w = 2 d2(w) 从表中读取的无偏常量(有关更多信息,请参见无偏常量 d2()、d3() 和 d4() 部分) - 移动极差中位数:
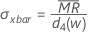
其中:

项 说明 MRi 第 i 个移动极差 MRbar̅ MRi 的中位数 w 在移动极差中使用的观测值个数。默认情况下,w = 2 d4(w) 从表中读取的无偏常量(有关更多信息,请参见无偏常量 d2()、d3() 和 d4() 部分) - 递差均方和平方根 (MSSD):
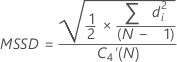
注意
如果更改默认设置并且不使用无偏常量,则用以下等式估计 σ组内:

项 说明 di 递差 C4(ni) 无偏常量(为合并标准差所定义) C4'(ni) 无偏常量 ≈ c4(ni)(有关详细信息,请参见“无偏常量 c4'()”部分) N 观测值总数 ni 第 i 个子组中的观测值个数
整体标准差

其中:
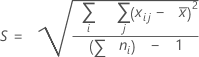
注意
默认情况下,Minitab 在估计 σ整体 时不使用无偏常量。σ整体 用 S 来估计。如果要使用无偏常量来估计整体标准差,则可以在执行能力分析时更改估计子对话框上的此选项。如果希望 Minitab 在默认情况下始终使用无偏常量,请选择,然后选择相应选项。
| 项 | 说明 |
|---|---|
| xij | 第 i 个子组中的第 j 个观测值 |
| x̅ | 过程均值 |
| ni | 第 i 个子组中的观测值个数 |
| C4 (N) | 无偏常量(为合并标准差所定义) |
| N(或 Σ ni) | 观测值总数 |
Box-Cox 变换
Box-Cox 变换估计 lambda 值(如下表所示),该值最小化标准式变换的变量的标准偏差。由此生成的变换是 Yλ(当 λ ҂ 0 时)及 ln Y(当 λ = 0时)。
Box-Cox 方法通过多种变换类型进行搜索。下表显示了一些常见的变换,其中 Y' 是数据 Y 的变换。
| Lambda (λ) 值 | 变换 |
|---|---|
 |
 |
 |
 |
 |
 |
 |
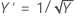 |
 |
 |
Johnson 变换的算法
Johnson 变换将选择三种分布系列中最优的一种系列来变换数据,使数据服从正态分布。
| Johnson 系列 | 变换函数 | 极差 |
|---|---|---|
| SB | γ + η ln [(x – ε) / (λ + ε – x)] | η,λ > 0,–∞ < γ < ∞,–∞ < ε < ∞,ε < x < ε + λ |
| SL | γ + η ln (x – ε) | η > 0,–∞ < γ < ∞,–∞ < ε < ∞,ε < x |
| SU | γ + η Sinh–1 [(x – ε) / λ],其中
Sinh–1(x) = ln [x + sqrt (1 + x2)] |
η,λ > 0,–∞ < γ < ∞,–∞ < ε < ∞,–∞ < x < ∞ |
该算法使用以下过程:
- 考虑了 Johnson 系统中几乎所有的潜在变换函数。
- 使用 Chou 等人描述的方法估计函数中的参数。1
- 使用变换函数变换数据。
- 计算变换数据的 Anderson-Darling 统计量和对应 p 值。
- 选择具有最大 p 值的变换函数,该 p 值大于您在变换对话框中指定的 p 值标准(默认值为 0.10)。否则,将没有适用的变换。
表示法
| 项 | 说明 |
|---|---|
| SB | 已限定变量的 Johnson 系列分布 (B) |
| SL | 使用对数正态变量的 Johnson 系列分布 (L) |
| SU | 未限定变量的 Johnson 系列分布 (U) |
有关 Johnson 变换的更多信息,请参见 Chou 等人的文献。1 Minitab 将使用 Anderson-Darling 检验替换该文本中使用的 Shapiro-Wilks 检验。
有关概率图、百分位数及其置信区间的信息,请转到个体分布标识中分布的方法和公式。
无偏常量 d2()、d3() 和 d4()
d2(N) 是正态总体分布(标准差 = 1)中 N 观测值的预期值。因此,如果 r 是正态分布(标准差 = σ)中 N 观测值的样本的极差,则 E(r) = d2(N)σ。
d3(N) 是正态分布(σ = 1)中 N 观测值的极差的标准差。因此,如果 r 是正态分布(标准差= σ)中 N 观测值的样本的极差,则 stdev(r) = d3(N)σ。
可使用下表查找给定值 N 的无偏常量(要确定 N 的值,请参考相关统计量的公式。)

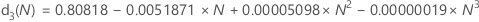
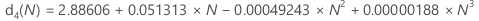
- D. J. Wheeler 和 D. S. Chambers(1992 年)。Understanding Statistical Process Control(了解统计过程控制)(第二版),SPC Press, Inc.
- H. Leon Harter(1960 年)。“Tables of Range and Studentized Range”(极差和学生化极差的表格)。The Annals of Mathematical Statistics(数理统计年鉴),第 31 卷,第 4 期,Institute of Mathematical Statistics,第 1122 到 1147 页。
| N | d2(N) | d3(N) | d4(N) |
|---|---|---|---|
| 2 | 1.128 | 0.8525 | 0.954 |
| 3 | 1.693 | 0.8884 | 1.588 |
| 4 | 2.059 | 0.8798 | 1.978 |
| 5 | 2.326 | 0.8641 | 2.257 |
| 6 | 2.534 | 0.848 | 2.472 |
| 7 | 2.704 | 0.8332 | 2.645 |
| 8 | 2.847 | 0.8198 | 2.791 |
| 9 | 2.97 | 0.8078 | 2.915 |
| 10 | 3.078 | 0.7971 | 3.024 |
| 11 | 3.173 | 0.7873 | 3.121 |
| 12 | 3.258 | 0.7785 | 3.207 |
| 13 | 3.336 | 0.7704 | 3.285 |
| 14 | 3.407 | 0.763 | 3.356 |
| 15 | 3.472 | 0.7562 | 3.422 |
| 16 | 3.532 | 0.7499 | 3.482 |
| 17 | 3.588 | 0.7441 | 3.538 |
| 18 | 3.64 | 0.7386 | 3.591 |
| 19 | 3.689 | 0.7335 | 3.64 |
| 20 | 3.735 | 0.7287 | 3.686 |
| 21 | 3.778 | 0.7242 | 3.73 |
| 22 | 3.819 | 0.7199 | 3.771 |
| 23 | 3.858 | 0.7159 | 3.811 |
| 24 | 3.895 | 0.7121 | 3.847 |
| 25 | 3.931 | 0.7084 | 3.883 |
| N | d2(N) |
|---|---|
| 26 | 3.964 |
| 27 | 3.997 |
| 28 | 4.027 |
| 29 | 4.057 |
| 30 | 4.086 |
| 31 | 4.113 |
| 32 | 4.139 |
| 33 | 4.165 |
| 34 | 4.189 |
| 35 | 4.213 |
| 36 | 4.236 |
| 37 | 4.259 |
| 38 | 4.28 |
| 39 | 4.301 |
| 40 | 4.322 |
| 41 | 4.341 |
| 42 | 4.361 |
| 43 | 4.379 |
| 44 | 4.398 |
| 45 | 4.415 |
| 46 | 4.433 |
| 47 | 4.45 |
| 48 | 4.466 |
| 49 | 4.482 |
| 50 | 4.498 |
无偏常量 c4() 和 c5()
c4()

c5()

表示法
| 项 | 说明 |
|---|---|
| Γ() | Gamma 函数 |
无偏常量 c4'()
可使用下表查找无偏常量 c4'() 的值,该常量在用于估计西格玛的 MSSD 方法的平方根的公式中使用。
| N | c4'(N) | N | c4'(N) | N | c4'(N) |
|---|---|---|---|---|---|
| 2 | 0.79785 | 41 | 0.990797 | 80 | 0.995215 |
| 3 | 0.87153 | 42 | 0.991013 | 81 | 0.995272 |
| 4 | 0.905763 | 43 | 0.991218 | 82 | 0.995328 |
| 5 | 0.925222 | 44 | 0.991415 | 83 | 0.995383 |
| 6 | 0.937892 | 45 | 0.991602 | 84 | 0.995436 |
| 7 | 0.946837 | 46 | 0.991782 | 85 | 0.995489 |
| 8 | 0.953503 | 47 | 0.991953 | 86 | 0.995539 |
| 9 | 0.958669 | 48 | 0.992118 | 87 | 0.995589 |
| 10 | 0.962793 | 49 | 0.992276 | 88 | 0.995638 |
| 11 | 0.966163 | 50 | 0.992427 | 89 | 0.995685 |
| 12 | 0.968968 | 51 | 0.992573 | 90 | 0.995732 |
| 13 | 0.971341 | 52 | 0.992713 | 91 | 0.995777 |
| 14 | 0.973375 | 53 | 0.992848 | 92 | 0.995822 |
| 15 | 0.975137 | 54 | 0.992978 | 93 | 0.995865 |
| 16 | 0.976679 | 55 | 0.993103 | 94 | 0.995908 |
| 17 | 0.978039 | 56 | 0.993224 | 95 | 0.995949 |
| 18 | 0.979249 | 57 | 0.99334 | 96 | 0.99599 |
| 19 | 0.980331 | 58 | 0.993452 | 97 | 0.996030 |
| 20 | 0.981305 | 59 | 0.993561 | 98 | 0.996069 |
| 21 | 0.982187 | 60 | 0.993666 | 99 | 0.996108 |
| 22 | 0.982988 | 61 | 0.993767 | 100 | 0.996145 |
| 23 | 0.98372 | 62 | 0.993866 | 101 | 0.996182 |
| 24 | 0.984391 | 63 | 0.993961 | 102 | 0.996218 |
| 25 | 0.985009 | 64 | 0.994053 | 103 | 0.996253 |
| 26 | 0.985579 | 65 | 0.994142 | 104 | 0.996288 |
| 27 | 0.986107 | 66 | 0.994229 | 105 | 0.996322 |
| 28 | 0.986597 | 67 | 0.994313 | 106 | 0.996356 |
| 29 | 0.987054 | 68 | 0.994395 | 107 | 0.996389 |
| 30 | 0.98748 | 69 | 0.994474 | 108 | 0.996421 |
| 31 | 0.987878 | 70 | 0.994551 | 109 | 0.996452 |
| 32 | 0.988252 | 71 | 0.994626 | 110 | 0.996483 |
| 33 | 0.988603 | 72 | 0.994699 | 111 | 0.996514 |
| 34 | 0.988934 | 73 | 0.994769 | 112 | 0.996544 |
| 35 | 0.989246 | 74 | 0.994838 | 113 | 0.996573 |
| 36 | 0.98954 | 75 | 0.994905 | 114 | 0.996602 |
| 37 | 0.989819 | 76 | 0.99497 | 115 | 0.996631 |
| 38 | 0.990083 | 77 | 0.995034 | 116 | 0.996658 |
| 39 | 0.990333 | 78 | 0.995096 | 117 | 0.996686 |
| 40 | 0.990571 | 79 | 0.995156 | 118 | 0.996713 |
| N | c4'(N) | N | c4'(N) | N | c4'(N) |
|---|---|---|---|---|---|
| 119 | 0.996739 | 160 | 0.997541 | 201 | 0.998016 |
| 120 | 0.996765 | 161 | 0.997555 | 202 | 0.998025 |
| 121 | 0.996791 | 162 | 0.99757 | 203 | 0.998034 |
| 122 | 0.996816 | 163 | 0.997584 | 204 | 0.998043 |
| 123 | 0.996841 | 164 | 0.997598 | 205 | 0.998052 |
| 124 | 0.996865 | 165 | 0.997612 | 206 | 0.998061 |
| 125 | 0.996889 | 166 | 0.997625 | 207 | 0.998070 |
| 126 | 0.996913 | 167 | 0.997639 | 208 | 0.998078 |
| 127 | 0.996936 | 168 | 0.997652 | 209 | 0.998087 |
| 128 | 0.996959 | 169 | 0.997665 | 210 | 0.998095 |
| 129 | 0.996982 | 170 | 0.997678 | 211 | 0.998104 |
| 130 | 0.997004 | 171 | 0.997691 | 212 | 0.998112 |
| 131 | 0.997026 | 172 | 0.997703 | 213 | 0.99812 |
| 132 | 0.997047 | 173 | 0.997716 | 214 | 0.998128 |
| 133 | 0.997069 | 174 | 0.997728 | 215 | 0.998137 |
| 134 | 0.997089 | 175 | 0.997741 | 216 | 0.998145 |
| 135 | 0.99711 | 176 | 0.997753 | 217 | 0.998152 |
| 136 | 0.99713 | 177 | 0.997765 | 218 | 0.99816 |
| 137 | 0.99715 | 178 | 0.997776 | 219 | 0.998168 |
| 138 | 0.99717 | 179 | 0.997788 | 220 | 0.998176 |
| 139 | 0.997189 | 180 | 0.9978 | 221 | 0.998184 |
| 140 | 0.997209 | 181 | 0.997811 | 222 | 0.998191 |
| 141 | 0.997227 | 182 | 0.997822 | 223 | 0.998199 |
| 142 | 0.997246 | 183 | 0.997834 | 224 | 0.998206 |
| 143 | 0.997264 | 184 | 0.997845 | 225 | 0.998214 |
| 144 | 0.997282 | 185 | 0.997856 | 226 | 0.998221 |
| 145 | 0.9973 | 186 | 0.997866 | 227 | 0.998228 |
| 146 | 0.997318 | 187 | 0.997877 | 228 | 0.998235 |
| 147 | 0.997335 | 188 | 0.997888 | 229 | 0.998242 |
| 148 | 0.997352 | 189 | 0.997898 | 230 | 0.99825 |
| 149 | 0.997369 | 190 | 0.997909 | 231 | 0.998257 |
| 150 | 0.997386 | 191 | 0.997919 | 232 | 0.998263 |
| 151 | 0.997402 | 192 | 0.997929 | 233 | 0.99827 |
| 152 | 0.997419 | 193 | 0.997939 | 234 | 0.998277 |
| 153 | 0.997435 | 194 | 0.997949 | 235 | 0.998284 |
| 154 | 0.99745 | 195 | 0.997959 | 236 | 0.998291 |
| 155 | 0.997466 | 196 | 0.997969 | 237 | 0.998297 |
| 156 | 0.997481 | 197 | 0.997978 | 238 | 0.998304 |
| 157 | 0.997497 | 198 | 0.997988 | 239 | 0.998311 |
| 158 | 0.997512 | 199 | 0.997997 | 240 | 0.998317 |
| 159 | 0.997526 | 200 | 0.998007 | 241 | 0.998323 |
| N | c4'(N) | N | c4'(N) | N | c4'(N) |
|---|---|---|---|---|---|
| 242 | 0.99833 | 283 | 0.998553 | 324 | 0.99872 |
| 243 | 0.998336 | 284 | 0.998558 | 325 | 0.998723 |
| 244 | 0.998342 | 285 | 0.998562 | 326 | 0.998727 |
| 245 | 0.998349 | 286 | 0.998567 | 327 | 0.99873 |
| 246 | 0.998355 | 287 | 0.998571 | 328 | 0.998734 |
| 247 | 0.998361 | 288 | 0.998576 | 329 | 0.998737 |
| 248 | 0.998367 | 289 | 0.99858 | 330 | 0.99874 |
| 249 | 0.998373 | 290 | 0.998585 | 331 | 0.998744 |
| 250 | 0.998379 | 291 | 0.998589 | 332 | 0.998747 |
| 251 | 0.998385 | 292 | 0.998593 | 333 | 0.998751 |
| 252 | 0.998391 | 293 | 0.998598 | 334 | 0.998754 |
| 253 | 0.998397 | 294 | 0.998602 | 335 | 0.998757 |
| 254 | 0.998403 | 295 | 0.998606 | 336 | 0.998761 |
| 255 | 0.998408 | 296 | 0.998611 | 337 | 0.998764 |
| 256 | 0.998414 | 297 | 0.998615 | 338 | 0.998767 |
| 257 | 0.99842 | 298 | 0.998619 | 339 | 0.99877 |
| 258 | 0.998425 | 299 | 0.998623 | 340 | 0.998774 |
| 259 | 0.998431 | 300 | 0.998627 | 341 | 0.998777 |
| 260 | 0.998436 | 301 | 0.998632 | 342 | 0.99878 |
| 261 | 0.998442 | 302 | 0.998636 | 343 | 0.998783 |
| 262 | 0.998447 | 303 | 0.99864 | 344 | 0.998786 |
| 263 | 0.998453 | 304 | 0.998644 | 345 | 0.99879 |
| 264 | 0.998458 | 305 | 0.998648 | 346 | 0.998793 |
| 265 | 0.998463 | 306 | 0.998652 | 347 | 0.998796 |
| 266 | 0.998469 | 307 | 0.998656 | 348 | 0.998799 |
| 267 | 0.998474 | 308 | 0.99866 | 349 | 0.998802 |
| 268 | 0.998479 | 309 | 0.998664 | 350 | 0.998805 |
| 269 | 0.998484 | 310 | 0.998668 | 351 | 0.998808 |
| 270 | 0.998489 | 311 | 0.998671 | 352 | 0.998811 |
| 271 | 0.998495 | 312 | 0.998675 | 353 | 0.998814 |
| 272 | 0.9985 | 313 | 0.998679 | 354 | 0.998817 |
| 273 | 0.998505 | 314 | 0.998683 | 355 | 0.99882 |
| 274 | 0.99851 | 315 | 0.998687 | 356 | 0.998823 |
| 275 | 0.998515 | 316 | 0.99869 | 357 | 0.998826 |
| 276 | 0.998519 | 317 | 0.998694 | 358 | 0.998829 |
| 277 | 0.998524 | 318 | 0.998698 | 359 | 0.998832 |
| 278 | 0.998529 | 319 | 0.998701 | 360 | 0.998835 |
| 279 | 0.998534 | 320 | 0.998705 | 361 | 0.998837 |
| 280 | 0.998539 | 321 | 0.998709 | 362 | 0.99884 |
| 281 | 0.998544 | 322 | 0.998712 | 363 | 0.998843 |
| 282 | 0.998548 | 323 | 0.998716 | 364 | 0.998846 |
| N | c4'(N) | N | c4'(N) | N | c4'(N) |
|---|---|---|---|---|---|
| 365 | 0.998849 | 411 | 0.998963 | 457 | 0.999054 |
| 366 | 0.998851 | 412 | 0.998965 | 458 | 0.999056 |
| 367 | 0.998854 | 413 | 0.998967 | 459 | 0.999058 |
| 368 | 0.998857 | 414 | 0.99897 | 460 | 0.999060 |
| 369 | 0.99886 | 415 | 0.998972 | 461 | 0.999061 |
| 370 | 0.998862 | 416 | 0.998974 | 462 | 0.999063 |
| 371 | 0.998865 | 417 | 0.998976 | 463 | 0.999065 |
| 372 | 0.998868 | 418 | 0.998978 | 464 | 0.999067 |
| 373 | 0.998871 | 419 | 0.99898 | 465 | 0.999068 |
| 374 | 0.998873 | 420 | 0.998982 | 466 | 0.999070 |
| 375 | 0.998876 | 421 | 0.998985 | 467 | 0.999072 |
| 376 | 0.998879 | 422 | 0.998987 | 468 | 0.999073 |
| 377 | 0.998881 | 423 | 0.998989 | 469 | 0.999075 |
| 378 | 0.998884 | 424 | 0.998991 | 470 | 0.999077 |
| 379 | 0.998886 | 425 | 0.998993 | 471 | 0.999078 |
| 380 | 0.998889 | 426 | 0.998995 | 472 | 0.999080 |
| 381 | 0.998892 | 427 | 0.998997 | 473 | 0.999082 |
| 382 | 0.998894 | 428 | 0.998999 | 474 | 0.999084 |
| 383 | 0.998897 | 429 | 0.999001 | 475 | 0.999085 |
| 384 | 0.998899 | 430 | 0.999003 | 476 | 0.999087 |
| 385 | 0.998902 | 431 | 0.999005 | 477 | 0.999088 |
| 386 | 0.998904 | 432 | 0.999007 | 478 | 0.999090 |
| 387 | 0.998907 | 433 | 0.999009 | 479 | 0.999092 |
| 388 | 0.998909 | 434 | 0.999011 | 480 | 0.999093 |
| 389 | 0.998912 | 435 | 0.999013 | 481 | 0.999095 |
| 390 | 0.998914 | 436 | 0.999015 | 482 | 0.999097 |
| 391 | 0.998917 | 437 | 0.999017 | 483 | 0.999098 |
| 392 | 0.998919 | 438 | 0.999019 | 484 | 0.9991 |
| 393 | 0.998921 | 439 | 0.999021 | 485 | 0.999101 |
| 394 | 0.998924 | 440 | 0.999023 | 486 | 0.999103 |
| 395 | 0.998926 | 441 | 0.999025 | 487 | 0.999104 |
| 396 | 0.998929 | 442 | 0.999027 | 488 | 0.999106 |
| 397 | 0.998931 | 443 | 0.999028 | 489 | 0.999108 |
| 398 | 0.998933 | 444 | 0.999030 | 490 | 0.999109 |
| 399 | 0.998936 | 445 | 0.999032 | 491 | 0.999111 |
| 400 | 0.998938 | 446 | 0.999034 | 492 | 0.999112 |
| 401 | 0.99894 | 447 | 0.999036 | 493 | 0.999114 |
| 402 | 0.998943 | 448 | 0.999038 | 494 | 0.999115 |
| 403 | 0.998945 | 449 | 0.999040 | 495 | 0.999117 |
| 404 | 0.998947 | 450 | 0.999042 | 496 | 0.999118 |
| 405 | 0.99895 | 451 | 0.999043 | 497 | 0.99912 |
| 406 | 0.998952 | 452 | 0.999045 | 498 | 0.999121 |
| 407 | 0.998954 | 453 | 0.999047 | 499 | 0.999123 |
| 408 | 0.998956 | 454 | 0.999049 | 500 | 0.999124 |
| 409 | 0.998959 | 455 | 0.999051 | ||
| 410 | 0.998961 | 456 | 0.999052 |
Gamma 表格
可使用下表为用于计算基准 Z 值的置信区间的 γN, 1 -α 的值,然后使用第二个公式获取 γN, 1 -α 的精确值。
| 1 -α | |||||
| N | 0.800 | 0.850 | 0.900 | 0.950 | 0.990 |
| 5 | 3.544 | 4.138 | 4.961 | 6.350 | 9.750 |
| 6 | 3.485 | 4.078 | 4.903 | 6.300 | 9.636 |
| 7 | 3.443 | 4.035 | 4.861 | 6.260 | 9.567 |
| 8 | 3.413 | 4.003 | 4.829 | 6.229 | 9.520 |
| 9 | 3.390 | 3.979 | 4.804 | 6.204 | 9.484 |
| 10 | 3.372 | 3.960 | 4.783 | 6.183 | 9.457 |
| 12 | 3.345 | 3.931 | 4.753 | 6.152 | 9.416 |
| 14 | 3.326 | 3.911 | 4.732 | 6.130 | 9.387 |
| 16 | 3.312 | 3.986 | 4.716 | 6.113 | 9.365 |
| 18 | 3.301 | 3.884 | 4.703 | 6.099 | 9.348 |
| 20 | 3.293 | 3.875 | 4.693 | 6.089 | 9.335 |
| 25 | 3.278 | 3.858 | 4.675 | 6.069 | 9.310 |
| 30 | 3.268 | 3.848 | 4.664 | 6.056 | 9.294 |
| 35 | 3.261 | 3.840 | 4.655 | 6.047 | 9.282 |
| 40 | 3.255 | 3.834 | 4.649 | 6.040 | 9.274 |
| 50 | 3.248 | 3.826 | 4.640 | 6.031 | 9.262 |
| 60 | 3.243 | 3.821 | 4.634 | 6.024 | 9.253 |
| 80 | 3.237 | 3.814 | 4.627 | 6.016 | 9.244 |
| 100 | 3.233 | 3.810 | 4.623 | 6.011 | 9.238 |
| >100 | 3.219 | 3.794 | 4.605 | 5.991 | 9.210 |
当 N 和 1 - a 未在表中列出时,可使用外推法来获取 γN, 1 -α 的值。例如,
- 对于介于 0.05 和 0.1 的 α 值(即 0.95 > 1 -α > 0.90)且 N = 10,

- 对于介于 60 和 80 的 N 值且 α = 0.80,
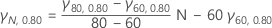
- 对于介于 0.05 和 0.1 的 α 值以及介于 60 和 80 之间的 N 值,使用第一个公式来计算 γ80, 1 -α 和 γ60, 1 -α 的值
