关于本主题
预期组内性能的 PPM < LSL

PPM < LSL 和 % < LSL 是概率的倍数:

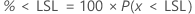
双侧置信区间
P(x < LSL) 的置信区间由以下公式给出:


其中
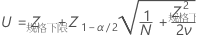


PPM < LSL 和 % < LSL 的置信区间通过将概率的置信区间乘以常数来获得。
PPM


%
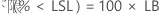
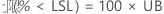
单侧置信边界
对于单侧边界,按如下公式计算:


Minitab 使用下面的方程求 p1:
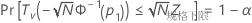
其中

表示法
表示法
| 项 | 说明 |
|---|---|
| 规格下限 | 规格下限 |
| 规格上限 | 规格上限 |
| 下限 | 下限 |
| 上限 | 上限 |
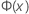 | 来自标准正态分布的累积分布函数 (CDF) |
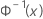 | 来自标准正态分布的逆 CDF |
 | 标准正态分布的第 (1 - α/2) 个百分位数 |
| α | 置信水平的 alpha |
 | 过程均值(从样本日期或历史值估计) |
| s | 子组内样本标准差 |
| N | 测量值的总数 |
| υ | s 的自由度 |
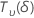 | 以非中心 t 分布形式分布的随机变量,具有 自由度和非中心参数 δ 自由度和非中心参数 δ |
预期组内性能的 PPM > USL
百万分数大于规格上限 (PPM > USL) 和百分比大于规格上限 (% > USL) 均从分数高于规格限的概率 (P(x > USL)) 中找到。

PPM > USL 和 % > USL 是概率的倍数:
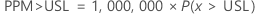
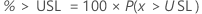
双侧置信区间
P(x > USL) 的置信区间由以下公式给出:


其中
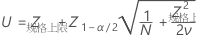


PPM > USL 和 % > USL 的置信区间通过将概率的置信区间乘以常数来获得。
PPM
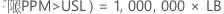
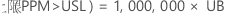
%
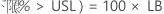
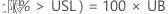
单侧置信边界
对于单侧边界,按如下公式计算:

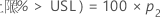
Minitab 使用下面的方程求 p1:
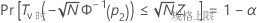
其中

表示法
| 项 | 说明 |
|---|---|
| 规格上限 | 规格上限 |
| PPM | 百万分数 |
| 下限 | 下限 |
| 上限 | 上限 |
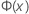 | 来自标准正态分布的累积分布函数 (CDF) |
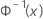 | 来自标准正态分布的逆 CDF |
 | 标准正态分布的第 (1 - α/2) 个百分位数 |
| α | 置信水平的 alpha |
 | 过程均值(从样本日期或历史值估计) |
| s | 子组内样本标准差 |
| N | 测量值的总数 |
| υ | s 的自由度 |
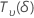 | 以非中心 t 分布形式分布的随机变量,具有 自由度和非中心参数 δ 自由度和非中心参数 δ |
预期组内性能的合计 PPM
根据子组内变异得出的超出规格限的预期百万分数为:

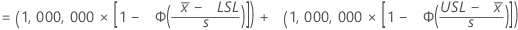
表示法
| 项 | 说明 |
|---|---|
| PPM | 百万分之 |
| LSL | 规格下限 |
| USL | 规格上限 |
| Φ (X) | 标准正态分布的累积分布函数 (CDF) |
 | 观测值的平均值 |
| s | 子组内标准差 |
在 LSL 和 USL 已知时预期组内性能的合计 PPM 的置信区间
总规格外百万分数和规格外百分比均从部件不在规格限内的概率中找到。
双侧置信区间
使用以下公式计算部件在规格外的概率的上限和下限:
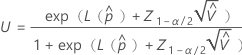
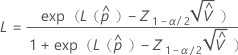
其中
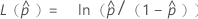
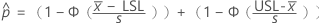
要计算  ,将公式中参数的样本估计值替换为
,将公式中参数的样本估计值替换为 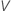 :
:



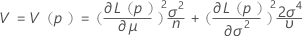
其中


总规格外 PPM 和总规格外百分比通过将概率的边界乘以常数获得。
PPM


%


单侧置信边界
使用以下公式计算部件在规格外的概率的上限:
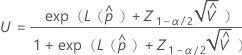
其中,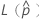 和
和  与双侧区间相同。
与双侧区间相同。
总规格外 PPM 和总规格外百分比的上限通过将概率的边界乘以常数来获得。
PPM
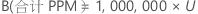
%

表示法
| 项 | 说明 |
|---|---|
| LSL | 规格下限 |
| USL | 规格上限 |
| PPM | 百万分数 |
| 下限 | 下限 |
| 上限 | 上限 |
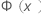 | 来自标准正态分布的累积分布函数 (CDF) |
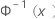 | 来自标准正态分布的逆 CDF |
 | 标准正态分布中的概率密度函数 (PDF) |
 | 标准正态分布的第 (1 - α /2) 个百分位数 |
| α | 置信水平的 alpha |
 | 过程均值(从样本日期或历史值估计) |
| s | 子组内样本标准差 |
| N | 测量值的总数 |
| υ | s的自由度 |
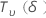 | 作为非中心 T 分布分布的随机变量,具有  自由度和非中心性参数 δ 自由度和非中心性参数 δ |
具有一个规格限的过程的预期组内性能的合计 PPM 的置信区间
对于仅具有规格下限 (LSL) 的过程,整体 PPM 或整体规格外总百分比与 PPM < LSL 或 % < LSL 的置信区间相同。请转到“预期组内性能的 PPM < LSL”部分。
对于仅具有规格上限 (USL) 的过程,整体 PPM 或整体规格外总百分比与 PPM > LSL 或 % > LSL 的置信区间相同。请转到“预期组内性能的 PPM > USL”部分。
