P 控制图
P 控制图绘制每个子组的不合格单元(也称缺陷品)的比率。中心线是所有子组缺陷品平均比率。控制限(设定为位于中心线上方和下方 3 个标准差的距离)显示子组比率中的预期变异量。
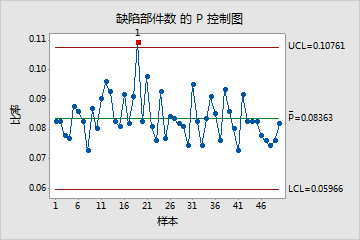
此 P 控制图显示,平均而言,任一天的产品缺陷率为 8%。第 19 天的缺陷产品比率失控,因为其对应的值不在预期变异限制范围内。
解释
可使用 P 控制图在视觉上监视缺陷百分比,以及确定缺陷百分比是否稳定并受控制。
红点表示至少未通过一个特殊原因检验且不受控制的子组。失控点表示过程可能不稳定,并且能力分析的结果可能不可靠。您应该在分析过程能力之前确定点失控的原因并消除特殊原因变异。
特殊原因检验
特殊原因检验评估每个控制图上的标绘点是否随机分布在控制限制之内。
解释
使用特殊原因检验,可以确定需要调查的观测值和您数据中的具体模式和趋势。每项检验特殊原因检验将检测您数据中的具体模式或者趋势,这将揭示过程不稳定性的不同方面。
- 1 个点,距离中心线超过 3 个 标准差(P)
- 检验 1 会标识与其他子组相比异常的子组。检验 1 是公认的、用于检测失控情况的必要检验。如果对过程中的较小偏移感兴趣,则您可以使用检验 2 来补充检验
1,以便创建一个具有更高敏感度的控制图。
- 连续 9 点在中心线同一侧(N)
- 检验 2 会标识过程变异中的偏移。如果对过程中的较小偏移感兴趣,则您可以使用检验 2 来补充检验 1,以便创建一个具有更高敏感度的控制图。
- 行内连续 6 点,全部递增或全部递减(S)
- 检验 3 检测趋势。该检验会查找值一致增加或减少的长序列连续点。
- 行内连续 14 点上下交错(F)
- 检验 4 检测系统变异。您希望过程中的变异模式随机,但是未通过检验 4 的一个点可能表明,变异模式是可预测的。
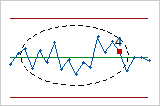
累积缺陷百分比图
累积缺陷百分比图上的点表示每个样本的缺陷品百分比均值。这些点将按样本收集顺序显示。中间水平线代表从所有样本计算的缺陷品百分比均值。上部和下部水平线代表缺陷品百分比均值的置信区间上下限。
解释
可使用累积百分比缺陷图确定是否具有足够样本,从而能够获得百分比缺陷的稳定估计值。
检查按时间排序的缺陷品百分比,以查看当收集更多样本时估计值如何变化。理想情况下,缺陷品百分比在几个样本后稳定,由沿缺陷品均值线的变平绘制点显示。
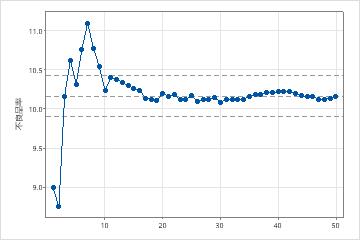
样本足够
在此图中,缺陷百分比沿缺陷百分比均值线稳定分布。因此,该能力研究包含了足够样本来稳定、可靠地估计缺陷百分比均值。

样本不够
在此图中,缺陷百分比不稳定。因此,该能力研究未包含足够样本来可靠地估计缺陷百分比均值。
二项图
二项图显示实测的缺陷品数与预期的缺陷品数。对角线显示完全服从二项分布时数据的分布位置。如果数据显著偏离这条线,则二项能力分析可能无法提供可靠结果。
注意
当子组大小相同时,Minitab 会显示二项图。如果子组大小不同,Minitab 会显示缺陷率图。有关详细信息,请参见关于缺陷率图的部分。
解释
可使用二项分布评估数据是否服从二项分布。
检查此图以确定绘制点是否大致遵循一条直线分布。如果不是,那么“数据是从二项分布采样的”这一假定可能是错误的。
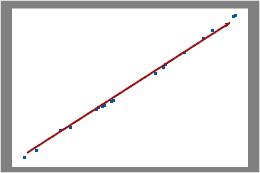
在此图中,数据点紧密地分布在这条线的周围。您可以假设数据服从二项分布。
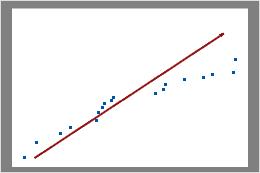
在此图中,数据点不沿图右上部附近的线分布。这些数据不服从二项分布,并且无法使用二项能力分析对其进行可靠评估。
重要信息
如果点不遵循线分布,则二项分布可能不适用于您的数据,而且能力分析可能会无效。
缺陷率图
缺陷品比率图显示子组中缺陷品的百分比以及每个子组的大小。中心线等于有缺陷的产品的平均概率。均值的置信上下限显示在中心线的上方和下方。
注意
Minitab 会在子组大小不同时显示缺陷率图。如果子组大小是恒定的,则 Minitab 会显示二项图。有关详细信息,请参见关于二项图的部分。
解释
使用缺陷品率图验证您的数据是否为二项数据,方法是检查缺陷品概率是否在不同样本数量之间保持不变。
检查此图以查看缺陷品百分比是否在整个样本数量中随机分布,或是否存在一种模式。如果数据随机分布在中心线周围,则可以推断数据服从二项分布。
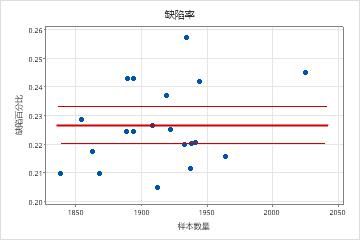
二项
在此图中,点随机分布在中心线周围。您可以假设数据服从二项分布。
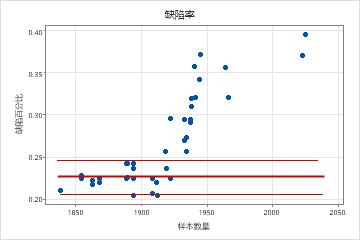
非二项分布
在此图中,模式不是随机的。对于大于 1900 的样本数量,缺陷率随样本数量增加而增高。此结果表明在样本数量和缺陷百分比之间存在相关性。因此,数据不服从二项分布,并且无法使用二项能力分析对其进行可靠估计。
直方图
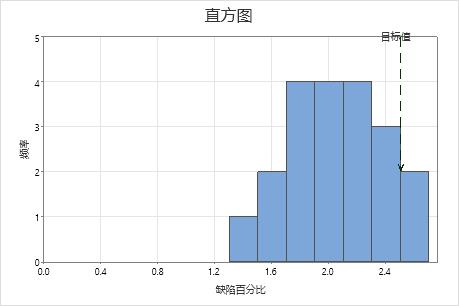
解释
可使用缺陷百分比直方图评估样本中缺陷百分比值的分布。
检查缺陷品百分比的峰值和展开。峰值表示最普通的值,并接近于缺陷品百分比的中心。评估展开以了解样本中缺陷品百分比的变化程度。
将目标值的基准线与直方图的条形进行比较。如果过程有能力,则大多数或所有直方图条形应在目标值的左侧。
缺陷百分比
缺陷品百分比(%缺陷品)是样本中无法接受的产品百分比。其他产品可分类为“合格”或“良好”。
解释
可使用缺陷百分比确定您的过程是否满足客户要求。
将缺陷品百分比值与目标缺陷品百分比值进行比较,以评估过程是否满足客户要求。如果缺陷品百分比值比目标值高,应改进过程。
还应将目标值与缺陷品百分比的置信区间上限进行比较。如果置信区间上限大于目标值,您将无法确信过程的缺陷品百分比低于目标。您可能需要更大的样本数量以更有信心地确定过程达到目标。
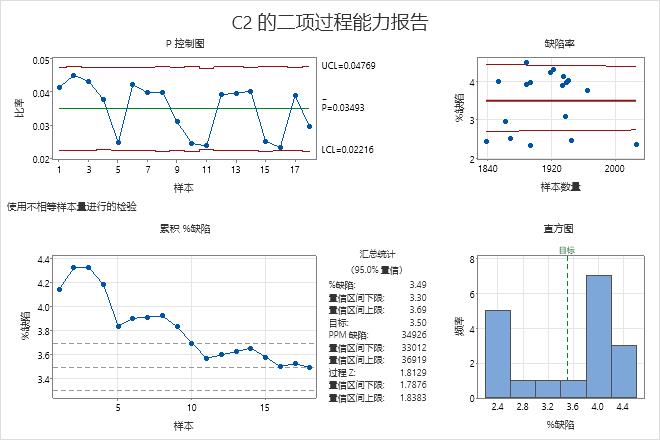
例如,假设客户服务过程的缺陷百分比不应超过 3.5%。在汇总统计表中,缺陷百分比是 3.49%,其小于目标值。但是,缺陷百分比的置信区间上限是 3.69%,其大于目标值。虽然缺陷百分比的样本估计值低于目标值,但是您需要更大的样本数量以便更有信心地确定过程的缺陷百分比是否满足客户要求。
目标值
目标缺陷品百分比值是您愿意接受的最大缺陷品百分比值。如果不指定此目标值,Minitab 将假定目标值是缺陷率百分比 0。
解释
将缺陷品百分比值与目标缺陷品百分比值进行比较,以评估过程是否满足客户要求。如果缺陷品百分比值比目标值高,应改进过程。
还应将目标值与缺陷品百分比的置信区间上限进行比较。如果置信区间上限大于目标值,您将无法确信过程的缺陷品百分比低于目标。您可能需要更大的样本数量以更有信心地确定过程达到目标。

例如,在汇总统计表中,缺陷百分比值是 3.46%,其小于目值标 (3.50%)。但是,缺陷百分比的置信区间上限是 3.66%,其大于目标值。虽然过程似乎满足要求,但是您需要更大的样本数量以便更有信心地确定缺陷百分比值是否低于目标值。
PPM 缺陷
缺陷品百万分数(缺陷品 PPM)估计预期的缺陷品百万分数。如果您从当前过程收集 1,000,000 个产品样本,缺陷品 PPM 是样品中的缺陷品的大致数量。
解释
将 PPM 缺陷值与客户要求进行比较,以确定您的过程是否需要改进。
还应考虑 PPM 缺陷的置信区间上限。如果置信区间上限大于允许的最大值,则无法确信过程满足客户要求。您可能需要更大的样本数量以更有信心地确定过程满足客户要求。

例如,在汇总统计表中,PPM 缺陷值是 34,926。如果客户要求 PPM 缺陷值低于 35,000,则该过程符合要求。但是,置信区间上限是 36,919,其大于客户的要求值。因此,您需要更大的样本数量以便更有信心地确定过程是否可接受。
过程 Z
过程 Z 是标准正态分布 N (0, 1) 中其右侧面积等于 P 均值(过程中有缺陷品的比率)的点。
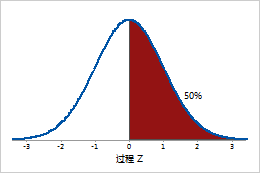
过程 Z 值 0 对应于缺陷品率 50%。
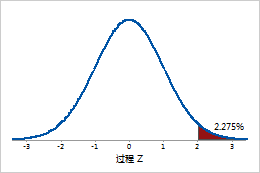
过程 Z 值 2 对应于缺陷品率 2.275%。
解释
可使用过程 Z 评估二元过程的西格玛能力。
较大的 Z 值表明过程执行得较好。理想情况下,过程 Z 值至少为 2。过程的目标值取决于您客户的缺陷品的后果。
置信区间 (CI)
置信区间是能力指数的可能值范围。置信区间由置信下限和置信上限定义。边界是通过确定样本估计值的边际误差来计算的。置信下限定义可能小于能力指数值的值。置信上限定义可能大于能力指数值的值。
Minitab 同时显示缺陷百分比、PPM 缺陷和过程 Z 的置信下限和置信上限。
解释
由于数据样本是随机的,因此从过程收集的不同样本不可能生成相同的能力指数估计值。要计算过程能力指数的实际值,您将需要分析由过程生成的所有项数据,而这是不可行的。您可以改为使用置信区间来确定能力指数值的可能范围。
在 95% 置信水平下,您可以 95% 地确信能力指数的实际值包含在置信区间内。也就是说,如果您从过程中收集 100 个随机样本,则可以预计 95 个样本生成的区间中包含能力指数的实际值。
置信区间有助于评估样本估计值的实际意义。如果可能,基于过程知识或行业标准将置信界限与基准值进行比较。
例如,某制造过程的允许最大缺陷比率是 0.50%。通过使用二项式分布过程能力分析,分析师获得缺陷百分比估计值 0.31%,这表明该过程有能力。缺陷百分比的置信区间上限为 0.48%。因此,分析师可以 95% 地确信缺陷百分比实际值不超过允许最大值,即使在考虑将会影响估值的随机抽样中变异也是如此。
