一家生产瓷砖的公司的质量工程师们想调查客户对地砖翘曲的投诉。为了确保生产质量,工程师在10天内每个工作日测量10块瓷砖的翘曲情况。翘曲测量的规格上限为 6 mm。工程师希望探索不同的选项,以找到一种合理的方法来估计过程的能力。
- 打开样本数据 瓷砖翘曲.MWX。
- 选择 。
- 在 单列中,输入翘曲程度。
- 在子组大小中,输入 10。
- 在规格上限中,输入 6。
- 选择 确定。
解释结果
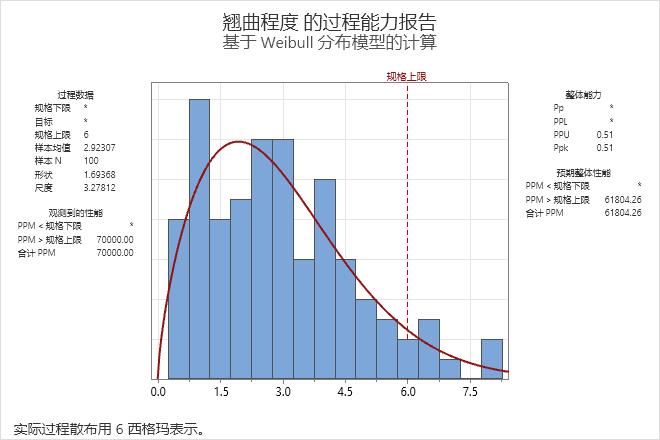
分析将显示提供合理拟合的第一种方法的能力报告。对于瓷砖的翘曲,结果使用 Weibull 分布。
对于这些数据,直方图右尾部的测量值似乎高于规格上限。因此,瓷砖的翘曲经常超过6毫米的规格上限。观察到的 PPM > USL 表明,每百万块瓷砖中有 70,000 块高于规格上限。整体Ppk为0.51,低于普遍接受的行业准则1.33。因此,工程师得出结论,该过程没有能力,不能满足客户要求。
分布结果表显示了方法的评估顺序。在第一行中,安德森-达令检验的结论是,由于 p 值小于 0.05,因此数据不服从显著性 0.05 水平的正态分布。在第二行中,安德森-达林检验的结论是,Weibull 分布与数据是合理的拟合,因为 p 值大于 0.05。能力结果适用于威布尔分布,因为威布尔分布是列表中提供合理拟合的第一种方法。
工程师使用过程知识来考虑 Weibull 分布是否是一个合理的选择。例如,威布尔分布的边界为 0。在数据中,0 是表示未变形图块的边界。
自动化能力分布结果: 翘曲程度
| 分布 | 位置 | 尺度 | 阈值 | 形状 | P | Ppk | Cpk |
|---|---|---|---|---|---|---|---|
| 正态 | 2.9231 | 1.7860 | 0.0100421 | 0.5743 | 0.5838 | ||
| Weibull* | 3.2781 | 1.6937 | >0.25 | 0.5133 | |||
| 对数正态 | 0.8443 | 0.7444 | <0.005 | 0.4242 | |||
| 最小极值 | 3.8641 | 1.9924 | <0.01 | 0.5362 | |||
| 最大极值 | 2.0958 | 1.4196 | 0.212835 | 0.5130 | |||
| Gamma | 1.2477 | 2.3428 | 0.238337 | 0.4851 | |||
| Logistic | 2.7959 | 1.0162 | 0.0127347 | 0.5799 | |||
| 对数 Logistic | 0.9097 | 0.4217 | <0.005 | 0.4090 | |||
| 指数 | 2.9231 | <0.0025 | 0.3780 | ||||
| 3 参数 Weibull | 2.9969 | 0.2099 | 1.5049 | 0.467097 | 0.4980 | ||
| 3 参数对数正态 | 1.3788 | 0.4184 | -1.4002 | 0.4961 | |||
| 3 参数 Gamma | 1.2314 | -0.0197 | 2.3898 | 0.4864 | |||
| 3 参数对数 Logistic | 1.3043 | 0.2700 | -1.0940 | 0.4656 | |||
| 2 参数指数 | 2.6679 | 0.2552 | <0.01 | 0.3982 | |||
| Box-Cox 变换 | 1.6237 | 0.5380 | 0.574337 | 0.5116 | 0.5214 | ||
| Johnson 变换 | 0.0112 | 0.9949 | 0.798895 | 0.4959 | |||
| 非参数 | 0.6187 |
